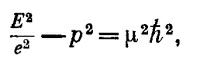| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Поле ядерных сил
Мне бы хотелось сделать еще несколько замечаний о неэлектромагнитной части массы ядерных частиц. Откуда берется большая доля их массы? Кроме электродинамических сил, существуют еще силы другого рода — ядерные силы, у которых есть своя собственная теория поля, хотя никому неизвестно, правильна она или нет. Эта теория также предсказывает энергию поля, которая для ядерных частиц дает массу, аналогичную электромагнитной. Ее можно называть «π-мезополевой массой». Она, по-видимому, очень велика, так как ядерные силы чрезвычайно мощны, и возможно, что именно они являются причиной массы тяжелых частиц. Однако теории мезонных полей находятся в весьма зачаточном состоянии. Даже в сравнительно хорошо развитой теории электромагнетизма мы видели, что, кроме первоначальных намеков, невозможно получить объяснение массы электрона. В мезонных же теориях мы в этом месте тоже терпим неудачу.
Мы видели, что поле может быть излучено, после чего оно существует независимо от источника. Это фотоны, и они описываются дифференциальным уравнением без источника:
Некоторые физики утверждают, что поле ядерных сил тоже должно иметь свои собственные «фотоны», роль которых, по-видимому, играют π-мезоны, и что они должны описываться аналогичным дифференциальным уравнением. (До чего же бессилен человеческий разум! Мы не можем придумать чего-то действительно нового и беремся рассуждать только по аналогии с тем, что знаем.) Таким образом, возможным уравнением для мезонов будет
где φ может быть каким-то другим четырехвектором или, возможно, скаляром. Далее выяснилось, что у π-мезона никакой поляризации нет, поэтому φ должно быть скаляром. Согласно этому простому уравнению, мезонное поле должно изменяться с расстоянием от источника как 1/r2, т. е. в точности как электрическое. Однако мы знаем, что радиус действия ядерных сил гораздо меньше, чего не может обеспечить нам это простое уравнение. Есть только один способ изменить положение вещей, не разрушая релятивистской инвариантности,— добавить или вычесть из даламбертиана произведение константы на поле φ. Итак, Юкава предположил, что свободные кванты ядерных сил могут подчиняться уравнению
где μ2 — некоторая постоянная, т. е. какой-то скаляр. (Поскольку П2 является скалярным дифференциальным оператором, то инвариантность не нарушится, если мы добавим к нему другой скаляр.)
которое было бы сферически симметрично относительно некоторой точки, скажем относительно начала координат. Если φ зависит только от r, то мы знаем, что
Таким образом, получается уравнение
Рассматривая теперь произведение (rφ) как новую функцию, мы имеем для нее уравнение, которое встречалось нам уже много раз. Решение ее имеет вид
Ясно, что при больших r поле φ не может быть бесконечным, поэтому нужно отбросить знак плюс в показателе экспоненты, после чего решение примет вид
Связывая теперь частоту с энергией, а волновое число с импульсом, как это делалось в конце гл. 34 (вып. 3), мы найдем соотношение
которое говорит, что масса «фотона» Юкавы равна μhlc. Если в качестве μ взять величину ≈1015м–1, которую дает наблюдаемый радиус действия ядерных сил, то масса оказывается равной 3·10–25 г, или 170 Мэв, что приблизительно равно наблюдаемой массе π-мезона. Таким образом, по аналогии с электродинамикой мы бы сказали, что π-мезон — это «фотон» поля ядерных сил. Однако теперь мы распространили идеи электродинамики в такую область, где они на самом деле могут оказаться и неверными. Мы вышли далеко за рамки электродинамики и очутились перед проблемой ядерных сил. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

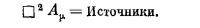
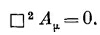
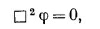

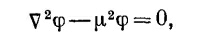
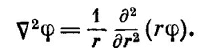
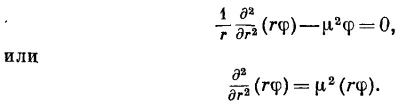
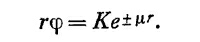

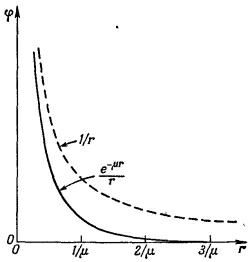 Эта функция называется потенциалом Юкавы. Для сил притяжения К должно быть отрицательным числом, величина которого подбирается так, чтобы удовлетворить экспериментально наблюдаемой величине ядерных сил.
Эта функция называется потенциалом Юкавы. Для сил притяжения К должно быть отрицательным числом, величина которого подбирается так, чтобы удовлетворить экспериментально наблюдаемой величине ядерных сил.