Главная >> Введение в теорию относительности § 19. Закон тяготения Эйнштейна
Рассмотренные выше выводы общей теории относительности были нами получены в предположении, что само поле тяготения заранее дано. Мы, однако, хорошо знаем, что поле тяготения создается материальными телами. Поэтому изучение физических процессов в «готовом» поле тяготения не исчерпывает всей задачи; нам нужно уметь находить и само поле, если распределение материи в пространстве задано.
Классический закон тяготения Ньютона утверждает, что сила тяготения в поле, созданном телом малых размеров (материальной точкой) убывает обратно пропорционально квадрату расстояния от этого тела. Этого правила достаточно, чтобы вычислить поле тяготения при совершенно произвольном распределении масс. Для этого данные массы разбивают на малые части, вычисляют силу тяготения от каждой такой массы в отдельности, а затем суммируют полученные результаты, складывая отдельные малые силы по правилу параллелограмма. Эта задача — чисто математическая; и математики немало потрудились, чтобы сделать ее решение удобным и изящным. Была разработана так называемая теория потенциала, которая в принципе позволяла решить любую задачу на определение поля тяготения. Основу этой теории составляет уравнение потенциала — математическое дифференциальное уравнение, являющееся непосредственным обобщением закона Ньютона на тела произвольной формы, размеров и плотности.
Несмотря на всю красоту и законченность этой теории, развитие теории относительности, как мы уже упоминали, привело к необходимости ее пересмотра. И Эйнштейн тотчас после создания специальной теории относительности принялся за решение этой задачи.
Здесь прежде всего нужно заметить, что к тому времени никаких опытных фактов, сколько-нибудь определенным образом говорящих о неточности закона Ньютона, не было. Наоборот, очень крупные успехи небесной механики, сопровождаемые такими триумфами, как предсказание существования новых планет — Нептуна и Плутона,— порождали все большую уверенность в том, что закон Ньютона выполняется всюду с абсолютной точностью. Решившись на изменение этого закона, Эйнштейн сразу же обрек себя на невозможность проверить свои результаты экспериментальным путем.
Опытные данные, которые могли бы подсказать, как, в какую сторону нужно менять теорию Ньютона, отсутствовали. Эйнштейн заменил их математическими идеями, выработанными специальной теорией относительности. И всего удивительнее то, что это почти фантастическое предприятие блестяще удалось.
После десятилетних поисков Эйнштейн нашел новые уравнения тяготения. Этот научный подвиг поистине колоссален. Общая теория относительности, несомненно, навсегда войдет в историю науки как одно из величайших достижений человеческого разума. В то же время крайняя математизация новой теории тяготения создавала впечатление, что вся она представляет собой совершенно произвольное построение, не имеющее отношения к реальной действительности. Физики привыкли каждый свой теоретический шаг подкреплять убедительными экспериментальными доказательствами. На математику продолжали смотреть как на простое орудие для вычислений; между тем, в теории относительности математические идеи и методы играют нисколько не меньшую роль, чем физические. Поэтому сначала почти никто теории Эйнштейна всерьез не принимал.
Тем более неожиданным оказалось первое ее экспериментальное подтверждение, связанное с искривлением световых лучей в поле тяготения. Неудивительно, что оно произвело потрясающее впечатление. Отношение физиков к теории относительности стало быстро меняться; ныне она является необходимой составной частью теоретической физики.
Рамки настоящей книги не позволяют, конечно, изложить сколько-нибудь полно основные руководящие идеи, с помощью которых Эйнштейн достиг столь невероятного успеха. В основных чертах они сводятся к следующим моментам.
Во-первых, нужно было исходить из того, что поле тяготения полностью определяется массой, энергией и импульсом находящейся в пространстве материи. В теории Ньютона фигурирует только масса; теория относительности довольно быстро приводит к выводу, что одной массы недостаточно. Поле тяготения существенно зависит от состояния движения материи и ее внутренней структуры.
Во-вторых, специальная теория относительности и принцип эквивалентности показывают, что поле тяготения можно полностью определить формулой собственного времени. Поэтому предстояло искать уравнения, выражающие коэффициенты этой формулы через массу, энергию и импульс материи. Коэффициентов этих в общем случае насчитывается десять; значит, речь шла о системе десяти уравнений с десятью неизвестными.
Исследование неинерциальных систем отсчета показало, что все физические законы допускают общековариантную формулировку; поэтому и уравнения тяготения можно было сразу же искать в ковариантном виде.
Далее, новые уравнения не должны, конечно, вступать в противоречие с теорией Ньютона; это означало, что для слабых полей тяготения должен получаться ньютоновский закон обратных квадратов. Уравнения тяготения должны тогда сводиться к классическому уравнению потенциала.
К этому добавлялись соображения о математическом характере искомых уравнений. Они должны принадлежать к тому же математическому типу, что п уравнение потенциала; входящие в них величины должны при перемене системы отсчета преобразовываться по определенным законам; они должны удовлетворять некоторым тождествам и т. д.
Огромную роль здесь сыграла разработанная Риманом геометрическая теория, о которой мы упоминали в начале книги. Оказалось, что основные понятия и соотношения римановой геометрии как нельзя лучше соответствуют основным понятиям и соотношениям теории относительности. Геометрический язык прочно укоренился в этой физической теории. Большое значение в ней имеет также тензорное исчисление.
В конце концов оказывается, что все эти отчасти физические, отчасти математические соображения приводят к уравнениям Эйнштейна почти с железной необходимостью.
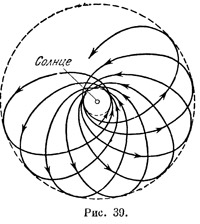
Основной задачей классической теории тяготения является так называемая задача Кеплера. Она состоит в определении движения «планеты» вокруг «Солнца», т. е. движения частицы исчезающе малой массы в поле тяготения, созданном массивным телом. Решение ее всем хорошо известно: частица будет двигаться по эллипсу, в одном из фокусов которого находится центральное тело; скорость ее движения определяется известным законом площадей. Понятно, что Эйнштейн в первую очередь принялся за решение этой же задачи на основании своих уравнений. Оказалось, что ее решение мало отличается от классического,— планета движется по кривой, весьма близкой к Эллипсу, но этот эллипс не остается неподвижным в пространстве, а медленно вращается в том же направлении, в каком движется планета (рис. 39), так что с течением времени планета описывает «розетку». Скорость вращения эллипса тем больше, чем ближе планета к Солнцу и чем более вытянута ее орбита. Вычисления сразу же показывают, что почти для всех планет это вращение орбиты безнадежно мало; лишь для орбиты Меркурия оно сравнительно велико — около 43 угловых секунд в столетие.
 |
Астрономам давно было известно, что орбиты всех планет медленно вращаются; однако это вращение не имеет никакого отношения к теории относительности. Оно объясняется воздействием планет друг на друга.
Притягиваясь друг к другу» планеты взаимно «возмущают» друг у друга орбиты, что и приводит к указанному вращению. Эти возмущения астрономы научились прекрасно учитывать; напомним, что Леверье доказал существование Нептуна как раз на основе изучения возмущений орбиты Урана.
Орбита Меркурия поворачивается в столетие на 532", т. е. в 12,5 раза быстрее, чем требует теория Эйнштейна. Понятно, что выловить среди множества возмущающих факторов чисто релятивистский эффект — задача не из легких. Но еще в середине прошлого века тот же Леверье специально занялся исследованием возмущений орбиты Меркурия и пришел к выводу, что не все они могут быть объяснены известными факторами. У него как раз остался «остаток» вращения примерно в 40" за столетие. Он тут же заподозрил существование новой планеты, находящейся к Солнцу еще ближе, чем Меркурий, и даже дал ей имя Вулкан. Однако на этот раз прославленный вычислитель ошибся — никакого Вулкана не существует.
Вычислив в 1915 году величину вращения орбиты Меркурия, Эйнштейн тотчас же обратил внимание на хорошее его совпадение с вычислениями Леверье. В дальнейшем результаты Леверье неоднократно уточнялись. Это привело к еще лучшему согласию, и в настоящее время вращение орбиты Меркурия расценивается как хорошее количественное подтверждение общей теории относительности.
Для орбиты Земли эффект вращения составляет около 4" в столетие и согласуется с теорией. Для остальных планет точность астрономических измерений не позволяет пока что сделать сколько-нибудь определенный вывод. В этой связи большой интерес представляют искусственные спутники Земли; подсчеты показывают, что у них вращения орбит могут быть определены с большой точностью. Этим пока исчерпываются экспериментальные подтверждения теории тяготения Эйнштейна, вернее, ее расхождений с теорией Ньютона. В то же время не известно ни одного явления, которое бы ей противоречило. В будущем, при соответствующем повышении точности измерений, вопрос о согласии теории Эйнштейна с действительностью станет, надо надеяться, гораздо определеннее.
Многие выводы из нового закона тяготения чрезвычайно интересны. Прежде всего, он полностью решает старый вопрос о скорости распространения тяготения. Оказывается, что тяготение распространяется со скоростью света. Мало того. Из закона Эйнштейна вытекает, что могут существовать гравитационные волны, т. е. колебания поля тяготения, распространяющиеся во все стороны, подобно электромагнитным волнам. Скорость этих волн также равна скорости света. Такие волны, между прочим, порождаются при своем движении всеми планетами солнечной системы, так что от нее непрерывно расходятся «круги» гравитационных волн. На эти волны расходуется некоторая энергия. Расчеты показывают, что эта энергия ничтожно мала — вся солнечная система излучает в виде энергии волн тяготения около 1 квт. К сожалению, гравитационные волны пока совершенно не поддаются экспериментальному исследованию.
Далее, в теории Ньютона поле тяготения зависит только от массы создающего его тела. Так, поле тяжелого шара не зависит от того, вращается этот шар или нет. В теории Эйнштейна поле тяготения существенно зависит от состояния движения тел. Поле тяготения вращающегося шара отличается от поля неподвижного шара тем, что в этом поле появляются дополнительные, правда, весьма слабые, силы, аналогичные центробежной силе и силе Кориолиса (сила Кориолиса — это та самая сила, которая на вращающейся Земле заставляет поворачиваться маятник Фуко, «закручивает» циклоны в земной атмосфере и заставляет реки в северном полушарии подмывать свой правый берег). Эти дополнительные силы быстро убывают с расстоянием от центрального тела — они обратно пропорциональны кубу этого расстояния. Полезно в этой связи вспомнить, что «настоящие» силы инерции во вращающейся системе растут пропорционально расстоянию от центра.
Имеются известные основания надеяться, что эти результаты общей теории относительности могут быть проверены путем наблюдений за движением искусственных спутников Земли.
Представляет большой интерес вопрос об энергии поля тяготения. Если мы рассмотрим, например, солнечную систему, то легко обнаружим, что суммарная энергия всех входящих в нее тел непрерывно меняется. В самом деле, планеты движутся вокруг Солнца неравномерно. Согласно закону площадей Кеплера, планета в перигелии, т. е. в ближайшей к Солнцу точке орбиты, движется быстрее, чем в противоположной точке — афелии. Поэтому ее кинетическая энергия непрерывно меняется. Это относится ко всем планетам, так что и суммарная энергия всех планет не остается постоянной.
Классическая физика обходила это затруднение тем, что вводила понятие потенциальной энергии. Планета в афелии обладает большей потенциальной энергией, чем в перигелии; при ее движении сумма кинетической и потенциальной энергии остается постоянной.
Однако при ближайшем рассмотрении понятие потенциальной энергии оказывается далеко не безупречным. Рассмотрим более простой пример. Пусть на поверхности Земли лежит груз. Поднимем его на некоторую высоту и укрепим его там снова неподвижно. При подъеме мы совершили некоторую работу, т. е. затратили некоторое количество энергии. Куда она девалась? Говорят, она перешла в потенциальную энергию. Но энергия сама по себе не существует; всякая энергия есть энергия определенного материального объекта. К какому же объекту относится потенциальная энергия?
Можно попытаться приписать ее грузу. Но ведь при подъеме внутреннее состояние этого груза не изменилось; каким он был, лежа на земле, таким он остался и после подъема. Приходится признать, что энергия тела может меняться без всякого изменения его состояния. А это противоречит всему духу современной физики. По той же причине нельзя приписать потенциальную энергию Земле.
Часто говорят, что потенциальная энергия относится к системе, состоящей из Земли и груза, а не к какому-либо отдельному телу. Но с точки зрения классической физики эта система включает в себя только два физических объекта — Землю и груз — и всякая ее энергия может относиться либо к одному, либо к другому телу, либо же быть как-то распределенной между ними. Как видим, ни то, ни другое, ни третье нельзя принять безоговорочно.
При переходе к теории относительности дело еще больше осложняется. Всякой энергии соответствует некоторая масса; какая же масса соответствует потенциальной энергии? Эта масса буквально «повисает в воздухе», так как ее нельзя отнести пи к грузу, ни к Земле.
В электродинамике эти вопросы давно разрешены. Выяснилось, что определенную энергию необходимо приписать самому электромагнитному полю. Тем самым потенциальная энергия оттуда полностью устраняется. Всякая энергия есть либо энергия тел, либо энергия поля. При движении заряженных тел в электромагнитном поле изменяется как энергия этих тел, так и энергия поля; но общая сумма энергии тел и поля остается постоянной. Энергия данного объема, занятого электромагнитным полем, определяется напряженностью поля, а закон сохранения энергии является прямым следствием уравнений Максвелла.
В теории тяготения следует, очевидно, поступить аналогичным образом. Полю тяготения необходимо приписать определенную энергию; при этом нужно позаботиться о том, чтобы закон сохранения энергии вытекал из уравнений тяготения. Оказывается, что уравнения Эйнштейна такую операцию допускают, так что и здесь потенциальная энергия приобретает конкретный смысл энергии поля тяготения. Вместе с тем сразу же обнаруживается, что энергетические свойства поля тяготения во многом отличаются от свойств других известных нам видов материи.
Имея дело, например, с жидкостью или газом, мы всегда можем приписать определенную энергию любому их объему; то же самое относится и к электромагнитному полю. При этом энергия всегда положительна, а если она в данном объеме обращается в нуль, то это означает, что здесь жидкость, газ или электромагнитное поле попросту отсутствуют. В случае поля тяготения дело обстоит иначе. Если мы рассмотрим в поле тяготения малый объем пространства, то по известным формулам можем рассчитать содержащуюся там энергию поля тяготения. Но, как известно, для этого объема можно выбрать систему отсчета, в которой поле тяготения исчезнет; вместе с тем обратится в нуль и энергия поля тяготения. Отсюда вытекает, что не имеет смысла говорить о количестве энергии тяготения, содержащейся в данном объеме; можно говорить лишь об энергии всего поля тяготения в целом. В случае солнечной системы мы можем сформулировать только такой закон: общая энергия всех тел системы и общего их поля тяготения остается постоянной.
Мы говорили здесь только об энергии поля тяготения; однако все сказанное почти дословно можно повторить и о массе, и о импульсе. Соответствующие законы сохранения могут быть сформулированы и для поля тяготения; при этом они также обладают такими же особенностями.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




