Главная >> Введение в теорию относительности § 20. Тяготение и геометрия
Начнем с исследования следующего мысленного эксперимента. Вообразим себе круглый диск, вращающийся вокруг своей оси в некоторой инерциальной системе отсчета S. Наряду с системой S мы рассмотрим также систему отсчета S`, вращающуюся вместе с диском, так что в этой системе диск неподвижен. Очевидно, система отсчета S` неинерциальна. Представим себе, что на диске находится наблюдатель, снабженный измерительной линейкой; пусть он желает измерить радиус и длину окружности диска. Каковы будут результаты этих измерений?
Будем следить за действиями нашего измерителя из инерциальной системы отсчета S. Допустим, что его линейка уложилась вдоль радиуса 100 раз. Когда он приступит к измерению длины окружности, он должен будет повернуть свою линейку по направлению окружной скорости края диска; при этом линейка тотчас испытает лоренцово сокращение. Если бы не этот эффект, то она уложилась бы по окружности примерно 628 раз; теперь же, став короче, она уложится, скажем, 640 раз. Что это значит?
Ведь мы хорошо знаем, что лоренцово сокращение есть чисто кинематический эффект, на самом деле сама линейка при повороте не подверглась никакому изменению. В системе отсчета S`, где диск и наблюдатель неподвижны, линейка как до поворота, так и после него имеет одну и ту же длину. Стало быть, в этой системе отсчета отношение длины окружности к радиусу равно не 2π, а другой величине. Величина эта зависит, очевидно, от скорости вращения системы отсчета, чем больше скорость, тем больше и отношение длины окружности к радиусу. Во вращающейся системе отсчета геометрия пространства оказывается неевклидовой. Геометрические свойства пространства относительны, в различных системах отсчета они различны.
Надо думать, что читатель достаточно подготовлен к тому, чтобы принять этот вывод без особого сопротивления. Ведь еще раньше, в § 9, занимаясь геометрией, пространства — времени, мы обнаружили, что различные системы отсчета производят различное «расщепление» единого четырехмерного пространства — времени на трехмерное пространство и одномерное время. Инерциальные системы отсчета «вырезают» из пространства — времени «плоские» пространственные «слои», внутренняя геометрия которых является евклидовой, вращающаяся система отсчета «расщепляет» пространство — время на «кривые» пространственные «слои». Поэтому здесь геометрия пространства оказывается неевклидовой, подобно внутренней геометрии сферической поверхности (вспомним рис. 1). Правда, в нашем обычном трехмерном евклидовом пространстве отсутствует поверхность, внутренняя геометрия которой совпадает с геометрией поверхности вращающегося диска; поэтому возможность наглядного представления здесь сильно ограничена.
Но если так, если уже в неинерциальных системах отсчета геометрия пространства не является евклидовой, то тем более этого следует ожидать в том случае, когда в пространстве имеется поле тяготения. Соответствующее исследование показывает, что это действительно так и есть. В частности, неевклидовой является геометрия пространства близ земной поверхности. Правда, отклонения от евклидовой геометрии здесь чрезвычайно малы и прямым измерениям пока что не поддаются, но наличие их несомненно.
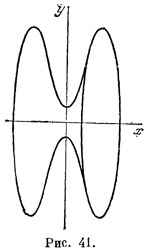 Геометрия нашего «земного» пространства уже допускает довольно наглядную иллюстрацию. Возьмем на обычной евклидовой плоскости оси координат х и у; единицы длины выберем для обеих осей точно по 1 см. Уравнение y = 0,291x2 + 0,86 в этой координатной системе определяет параболу,изображенную 1/4 натуральной величины па рис. 40. Представим себе эту кривую продолженной до бесконечности. Пусть, далее, она вращается вокруг оси х. При этом наша парабола опишет поверхность, изображенную на рис. 41 (напоминаем, что все построения производятся в евклидовом пространстве). Рассмотрим участок этой поверхности, отстоящий от оси вращения на расстоянии, равном радиусу Земли, т. е. примерно 6370 км. Геометрия нашего «земного» пространства уже допускает довольно наглядную иллюстрацию. Возьмем на обычной евклидовой плоскости оси координат х и у; единицы длины выберем для обеих осей точно по 1 см. Уравнение y = 0,291x2 + 0,86 в этой координатной системе определяет параболу,изображенную 1/4 натуральной величины па рис. 40. Представим себе эту кривую продолженной до бесконечности. Пусть, далее, она вращается вокруг оси х. При этом наша парабола опишет поверхность, изображенную на рис. 41 (напоминаем, что все построения производятся в евклидовом пространстве). Рассмотрим участок этой поверхности, отстоящий от оси вращения на расстоянии, равном радиусу Земли, т. е. примерно 6370 км.
Оказывается, что внутренпяя геометрия этого участка построенной нами кривой поверхности совпадает с внутренней геометрией вертикальной плоскости вблизи земной поверхности. Так как расстояние от оси вращения очень велико, то паша поверхность искривлена здесь очень слабо, и ее внутренняя геометрия весьма мало отличается от евклидовой.
Можно добавить к этому, что геометрия поверхности сферы с центром, совпадающим с центр ом,земного шара, не отличается от геометрии сферической поверхности в обычном евклидовом пространстве.
Мы до сих пор говорили только о геометрии пространства; однако можно рассматривать также геометрию четырехмерного пространства — времени, подобно тому, как мы это делали в § 9. Если поле тяготения отсутствует, то эта четырехмерная геометрия будет евклидовой, так как в этом случае всегда можно выбрать инерциальную систему отсчета. В поле тяготения этого сделать уже нельзя; эта значит, что геометрия пространства — времени в целом не будет евклидовой. Говорят, что в поле тяготения пространство—время обладает кривизной. Однако этому выражению не следует придавать слишком буквальный смысл. Ничего, кроме невозможности выбрать инерциальную систему отсчета во всем пространстве сразу, этот термин по существу не означает.
Итак, характер геометрии пространства — времени определяется полем тяготения; само же поле тяготения создается распределенной в пространстве материей.
Таким образом, геометрические свойства как трехмерного пространства, так и четырехмерного пространства — времени целиком определяются находящейся в пространстве материей. Установление этого факта является одним из самых замечательных достижений общей теории относительности. Гениальные догадки Лобачевского и Римана блестяще подтвердились. Геометрические свойства пространства неотделимы от физических свойств наполняющей его материи; проблема геометрии реального мира есть проблема прежде всего физическая.
Аксиомы евклидовой геометрии в применении к реальному физическому пространству справедливы далеко не всегда, а лишь в инерциальных системах отсчета при отсутствии поля тяготения. Во всех остальных случаях они являются лишь известным приближением к действительности.
Вблизи тяжелых материальных тел пространство — время «искривляется»; это «искривление» воспринимается нами как поле тяготения. Оно сказывается, во-первых, в том, что движение «по инерции» не является уже равномерным и прямолинейным и, во-вторых, в том, что геометрия пространства перестает быть евклидовой. То, что первое явление для нас гораздо заметнее, чем второе, объясняется большой величиной скорости света.
Все известные нам явления, связанные с всемирным тяготением: законы падения тел, законы Кеплера, отклонение светового луча вблизи тяжелых тел, гравитационное красное смещение и т. д., могут быть полностью объяснены этим «искривлением» пространства — времени. Однако теперь уже довольно ясно, что общая теория относительности далеко не исчерпывает свойств пространства — времени и свойств тяготения. Развитие квантовой теории полей уже привело к существенно новым взглядам на физический вакуум, выдвинута гипотеза о существовании своеобразных частиц тяготения — гравитонов. Правда, эта новая теория еще далека от завершения и пока совершенно не ясно, какой она примет в конце концов вид, но нельзя сомневаться в том, что теория относительности не является «окончательной истиной в последней инстанции».
Но какова бы ни была эта новая теория, современная теория относительности никогда уже не будет опровергнута, так же, как она сама не опровергла классической ньютоновской механики. Она навсегда сохранит свое значение как теория, дающая в высшей степени точное количественное объяснение большому кругу физических явлений.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Геометрия нашего «земного» пространства уже допускает довольно наглядную иллюстрацию. Возьмем на обычной евклидовой плоскости оси координат х и у; единицы длины выберем для обеих осей точно по 1 см. Уравнение y = 0,291x2 + 0,86 в этой координатной системе определяет параболу,изображенную 1/4 натуральной величины па рис. 40. Представим себе эту кривую продолженной до бесконечности. Пусть, далее, она вращается вокруг оси х. При этом наша парабола опишет поверхность, изображенную на рис. 41 (напоминаем, что все построения производятся в евклидовом пространстве). Рассмотрим участок этой поверхности, отстоящий от оси вращения на расстоянии, равном радиусу Земли, т. е. примерно 6370 км.
Геометрия нашего «земного» пространства уже допускает довольно наглядную иллюстрацию. Возьмем на обычной евклидовой плоскости оси координат х и у; единицы длины выберем для обеих осей точно по 1 см. Уравнение y = 0,291x2 + 0,86 в этой координатной системе определяет параболу,изображенную 1/4 натуральной величины па рис. 40. Представим себе эту кривую продолженной до бесконечности. Пусть, далее, она вращается вокруг оси х. При этом наша парабола опишет поверхность, изображенную на рис. 41 (напоминаем, что все построения производятся в евклидовом пространстве). Рассмотрим участок этой поверхности, отстоящий от оси вращения на расстоянии, равном радиусу Земли, т. е. примерно 6370 км.