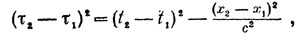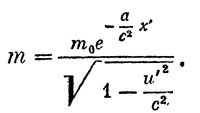Главная >> Введение в теорию относительности § 15. Инерциальные и неинерциальные системы отсчета
До сих пор мы пользовались исключительно такими системами отсчета, которые движутся равномерно и прямолинейно. Теперь настало время рассмотреть это условие более детально. Прежде всего необходимо выяснить, что следует понимать под равномерным п прямолинейным движением. Ведь мы давно знаем, что нет никакого смысла говорить о движении какого-либо тела самого по себе; можно говорить лишь о движении одного тела по отношению к другому. По отношению к какому же телу наши системы отсчета движутся равномерно и прямолинейно?
Вопрос этот самым тесным образом связан с законом инерции. Тело, на которое не действуют силы, движется равномерно и прямолинейно. Спрашивается, к какому телу, к какой системе отсчета надлежит относить это движение? Брошенный вверх камень относительно земной поверхности движется с переменной скоростью; однако относительно другого свободно падающего камня он движется равномерно и прямолинейно. Без указания определенной системы отсчета закон инерции не имеет смысла. Какую же систему отсчета имел в виду Ньютон, формулируя закон инерции?
По этому вопросу Ньютон высказался достаточно определенно. В своих «Началах» он заявил, что существует некое «абсолютное пространство», к которому и следует относить движение всех тел. Правда, он не указал, как определить, движется или покоится данное тело относительно этого пространства. Дальнейшее развитие физики привело к отказу от представления о существовании такой «абсолютной» системы отсчета; последним ее остатком был эфир. Но как же все-таки быть с законом инерции?
Опыт показывает, что все тела, освобожденные от действия внешних сил, движутся друг относительно друга равномерно и прямолинейно. Отсюда вытекает, что существуют системы отсчета, в которых закон инерции допускает ньютоновскую формулировку — свободное тело движется с постоянной скоростью. Такие системы отсчета называются инерциальными. Нетрудно понять, что две инерциальные системы отсчета движутся одна относительно другой равномерно и прямолинейно. Все другие системы отсчета будут неинерциальными характерной их особенностью является кажущееся нарушение закона инерции. Так, например, относительно Земли Солнце движется по окружности; в то же время не существует сил, которые заставляют его отклоняться от прямолинейного движения. Стало быть, в системе отсчета, связанной с Землей, ньютоновская формулировка закона инерции теряет силу.
Конечно, закон инерции, являясь общим законом природы, выполняется всегда и всюду, независимо от того, в какой системе отсчета мы желаем рассматривать движение тел. Но математическая его формулировка зависит от системы отсчета: относительно Земли его надо формулировать иначе, чем относительно Солнца. Проще всего закон инерции, а вместе с ним и все другие физические законы формулируются именно в инерциальных системах отсчета. Поэтому такие системы играют в физике исключительно важную роль. В частности, все наши предыдущие рассмотрения проводились в инерциальных системах. Следует отдавать себе полный отчет в том, что самый факт существования инерциальных систем отсчета есть определенное свойство пространства и времени. Мы скоро увидим, что такие системы могут существовать не всегда и не везде. Та часть теории относительности, которая опирается на возможность существования инерциальных систем отсчета, носит название специальной или частной теории относительности. Именно эта теория и была создана к 1905 году Лоренцом, Пуанкаре и Эйнштейном. В дальнейшем, работая над уточнением закона всемирного тяготения, Эйнштейн разработал общую теорию относительности, в которой возможность построения инерциальных систем отсчета уже не предполагается. Эта теория значительно сложнее как по характеру физических идей, так и по математическому аппарату. Поэтому мы вынуждены будем ограничиться лишь простейшими выводами общей теории относительности и отказаться от всяких попыток дать какие-либо доказательства; читателю придется во всем верить автору на слово.
Мы начнем с рассмотрения неинерциальных систем отсчета в рамках специальной теории относительности. Для этого попытаемся построить пример такой системы. С этой целью воспользуемся изученным нами ранее равноускоренным движением. Вообразим для конкретности ракету, летящую в мировом пространстве равноускоренно относительно некоторой инерциальной системы отсчета S. Построим новую систему отсчета S, в которой наша ракета была бы неподвижной.
Всякая система отсчета должна для каждого события давать его пространственно-временные координаты; мы, следовательно, должны установить на нашей ракете соответствующие приборы. Одним из таких приборов нам послужит радиолокатор. Будем посылать из ракеты во все стороны радиоимпульсы и фиксировать моменты их отправления и возврата после отражения от тех или иных тел. Считая скорость света по-прежнему постоянной и равной с, мы можем таким образом вычислить расстояние до точки отражения, а также и самый момент отражения. Разумеется, моменты отправления и возвращения сигналов мы будем отсчитывать по имеющимся в ракете часам, т. е. по собственному времени ракеты. Таким образом, вторым прибором будут часы, которые, как всегда, считаются идеальными.
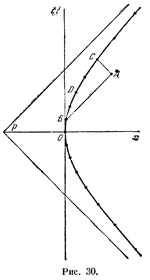 Выберем на чертеже (рис. 30) оси x и ct для системы отсчета S. Нанесем на этот чертеж мировую линию нашей ракеты. Из § 12 мы знаем, что это будет гипербола, асимптоты которой пересекаются в точке Р (см. рис. 26). Мы будем рассматривать эту гиперболу целиком, считая, что ракета двигалась равноускоренно и до момента, который мы выбрали в качестве начала отсчета времени; в это время она, очевидно, двигалась справа налево. В точке О ракета на мгновенье останавливается, а затем движется в обратную сторону. Выберем на чертеже (рис. 30) оси x и ct для системы отсчета S. Нанесем на этот чертеж мировую линию нашей ракеты. Из § 12 мы знаем, что это будет гипербола, асимптоты которой пересекаются в точке Р (см. рис. 26). Мы будем рассматривать эту гиперболу целиком, считая, что ракета двигалась равноускоренно и до момента, который мы выбрали в качестве начала отсчета времени; в это время она, очевидно, двигалась справа налево. В точке О ракета на мгновенье останавливается, а затем движется в обратную сторону.
В том же § 12 приведена формула, дающая возможность вычислять собственное время ракеты. Пользуясь этой формулой, мы можем нанести на мировую линию ракеты точку, отвечающую любому заданному моменту собственного времени. Выберем какой-либо фиксированный отрезок собственного времени и нанесем на нашу гиперболу точки, отстоящие друг от друга на такой отрезок (см. рис. 30).
Пусть в тот момент, когда ракета находится в точке В, радиолокатор излучает импульс, который, отразившись в точке А от какого-то тела, возвращается обратно в момент С. Из чертежа видно, что между мохментами отправки и приема сигнала прошло четыре единицы собственного времени.Так как скорость света в обе сторопы одинакова, мы заключаем, что, во-первых, отражение произошло в момент времени, средний между В и С, т. е. событие А происходит одновременно (в системе отсчета S`) с событием D, которое лежит на мировой лнниц ракеты, и следовательно, может быть зафиксировано непосредственно. Во-вторых, расстояние точки А от ракеты равно, очевидно, двум единицам времени, умноженным на скорость света. Тем самым координаты события А в системе отсчета S` полностью определены.
Какие же события в системе отсчета S` имеют одинаковые пространственные координаты? Другими словами, как должно двигаться в системе S тело, чтобы в системе S` его можно было считать неподвижным? Для нахождения мировой линии такого тела нужно, очевидно, поступить следующим образом. Предположим, что мы хотим найти мировую линию тела, находящегося справа от ракеты на расстоянии, равном единице времени, умноженной на скорость света. Радиоимпульс, выпущенный из локатора вправо, вернется после отражения от рассматриваемого тела через две единицы времени. Берем на нашей гиперболе аа две точки, отстоящие друг от друга на две единицы собственного времени, проводим из нижней точки световую прямую вверх, из верхней точки — вниз. Точка пересечения и будет одной из мировых точек искомого тела. Повторяя это построение с различными точками достаточно большое число раз, мы и получим всю мировую линию (рис. 31). Это, как можно доказать, будет снова гипербола. Значит, тело, неподвижное в системе отсчета S`, в системе S движется равноускоренно, в чем, конечно, нет ничего удивительного. Несколько неожиданно лишь то, что ускорение этого тела не равно ускорению а ракеты. Оказывается, что если х`— пространственная координата нашего «неподвижного» тела, то его ускорение b в системе отсчета S равно
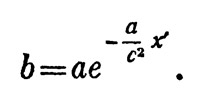 |
Аналогично можно построить и мировую линию неподвижного в системе S` тела, расположенного левее ракеты. Пространственная координата его будет уже отрицательной. Здесь мы сталкиваемся с любопытным обстоятельством. Какой бы большой отрицательной координатой мы ни задались, мировая линия соответствующего тела будет дежать внутри угла, образованного световыми линиями PQ и PR (см. рис. 31). Все наши гиперболы неограниченно (асимптотически) приближаются к этим прямым, никогда, однако, их не пересекая. Это значит, что наша система отсчета не способна охватить всего пространства — времени. Ни одно из событий, расположенных вне этого угла, не может быть зарегистрировано системой S.
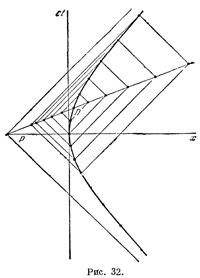
Рассмотрим теперь события, одновременные в системе отсчета S`. Пусть D — событие, происходящее в самой ракете. Чтобы построить мировую точку события, с ним одновременного, нужно, как мы уже выяснили, отложить от точки D вверх и вниз по гиперболе одинаковые отрезки собственного времени и провести из них световые линии (рис. 32). Точки пересечений этих линий и будут искомыми. Беря разные отрезки собственного времени, можем построить сколько угодно точек, отвечающих одновременным с D событиям. Все они лежат на прямой, проходящей через точки D и Р. Эта прямая будет «моментальным снимком» пространства, произведенным системой отсчета S`.
 |
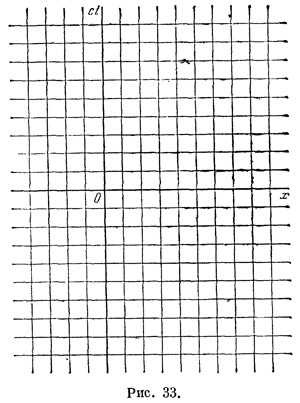
Выберем теперь некоторые определенные единицы времени и длины как для системы S, так и для системы S`. Если мы для системы отсчета S нанесем на график мировые линии неподвижных тел, отстоящих друг от друга на единицу длины, а также «моментальные снимки» пространства, произведенные один после другого через равные промежутки времени, отвечающие выбранной единице времени, то получим прямоугольную сетку (рис. 33). Это будет координатная сетка, «накладываемая» на пространство — время системой отсчета S.
Аналогичное построение для системы отсчета S` даст совсем другую координатную сетку (рис. 34). Прежде всего, эта сетка уже не является прямолинейной — временнонодобные координатные линии ее являются гиперболами. Пространственноподобные линии суть прямые; ось х` совпадает с осью х, но, как нетрудно убедиться, масштабы длины по этим осям совсем различны.
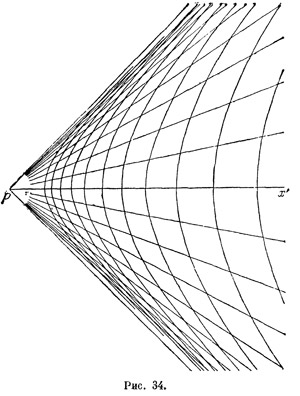 |
Особенно резко это обнаруживается на координатах точки Р —- в системе отсчета S ее пространственная координата равна — с2/а, а в системе S`— минус бесконечности (— ∞).
Таким образом, переход к неинерциальным системам отсчета требует введения криволинейных координат для пространства — времени. В разобранном нами случае система S` «вырезает» из пространства — времени «прямолинейные» пространственные «слои», но нетрудно представить себе возможность таких систем отсчета, которые будут «вырезать» кривые пространственные «слои». Следовательно, надо быть готовым к тому, что в неинерциальных системах отсчета пространство может оказаться неевклидовым. К этому вопросу мы в дальнейшем еще вернемся.
Мы уже говорили о том, что характерным признаком неинерциальности системы отсчета является неньюотонова формулировка закона инерции. Как же теперь его сформулировать? Для этого нам придется вспомнить основное свойство собственного времени. Из всех мировых линий, соединяющих две данные мировые точки, наибольший интервал собственного времени даст линия, отвечающая движению по инерции. Такая формулировка, как уже в свое время отмечалось, не зависит ни от какой системы отсчета; в частности, она сохраняет полную силу и для неинерциальных систем.
Для того чтобы иметь возможность применить этот закон для решения конкретных задач, необходимо, во-первых, знать, как вычислять собственное время вдоль произвольной мировой линии в любой системе отсчета, и, во-вторых, уметь находить среди мировых линий те, которые отвечают максимуму собственного времени. К сожалению, обе эти задачи требуют для своего решения средств высшей математики. Что касается первой задачи, то дело здесь обстоит следующим образом.
Мы уже знаем, что в любой инерциальной системе отсчета интервал собственного времени выражается следующей формулой:
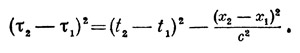 |
Здесь x1, t1 и х2, t2— координаты двух близких (точнее, бесконечно близких) событий. Чтобы вычислить интервал собственного времени вдоль любой мировой линии, нужно разбить ее на достаточно малые участки, к каждому из них применить эту формулу и просуммировать полученные результаты. Получится некоторое приближенное решение; оно будет тем точнее, чем мельче мы раздробим отрезок мировой линии. Совершенно точный ответ получается с помощью интегрального исчисления. Для того чтобы вычислить собственное время в неинерциальной системе отсчета S`, нужно в ту же формулу вместо х и t подставить выражения этих величин через координаты х` и t` системы отсчета S`. Выражения эти аналогичны формулам преобразований Лоренца — они служат для перехода от системы S к системе S`. Преобразования Лоренца обладают тем свойством, что они не меняют формулы собственного времени; в общем случае, при переходе к неинерциальным системам отсчета, это обстоятельство уже не имеет места. Мы получим совершенно другую формулу; в разобранном выше случае «равноускоренной» системы отсчета собственное время дается уравнением

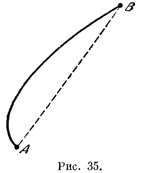 Пусть даны две мировые точки А и В. Соединим их отрезком какой-нибудь мировой линии (рис. 35), Вычислим вдоль этого отрезка интервал собственного времени. Для этого мы можем воспользоваться любой системой отсчета — результат от этого зависеть не будет. Но от самой мировой линии результат зависит: взяв другую линию, получим другой интервал. Среди всевозможных линий, соединяющих точки А и В, существует одна-единственная, для которой соответствующий интервал собственного времени принимает наибольшее возможное значение. Это будет мировая линия тела, которое движется по инерции. Как ее найти? В инерци-альной системе отсчета задача решается исключительно просто — эта линия будет прямой. Но отыскать ее можно и в любой другой системе отсчета. Решением подобных задач о нахождении линий, для которых определенная величина принимает наибольшее или наименьшее значение, занимается особая математическая дисциплина — вариационное исчисление. Воспользовавшись методами вариационного исчисления, мы и найдем мировую линию тела, двигающегося по инерции. Пусть даны две мировые точки А и В. Соединим их отрезком какой-нибудь мировой линии (рис. 35), Вычислим вдоль этого отрезка интервал собственного времени. Для этого мы можем воспользоваться любой системой отсчета — результат от этого зависеть не будет. Но от самой мировой линии результат зависит: взяв другую линию, получим другой интервал. Среди всевозможных линий, соединяющих точки А и В, существует одна-единственная, для которой соответствующий интервал собственного времени принимает наибольшее возможное значение. Это будет мировая линия тела, которое движется по инерции. Как ее найти? В инерци-альной системе отсчета задача решается исключительно просто — эта линия будет прямой. Но отыскать ее можно и в любой другой системе отсчета. Решением подобных задач о нахождении линий, для которых определенная величина принимает наибольшее или наименьшее значение, занимается особая математическая дисциплина — вариационное исчисление. Воспользовавшись методами вариационного исчисления, мы и найдем мировую линию тела, двигающегося по инерции.
Но такое решение, когда заранее указаны две точки и требуется отыскать линию, их соединяющую, не всегда может нас удовлетворить. Интересно как-то сразу охарактеризовать все мировые линии тел, движущихся по инерции, найти условия, которым должны всегда подчиняться такие линии. Такие условия также могут быть найдены средствами вариационного исчисления. Они формулируются в виде дифференциальных уравнений. Решив эти уравнения, мы тем самым найдем все искомые мировые линии. Нужно, правда, заметить, что решение дифференциальных уравнений — задача нелегкая и лишь в исключительных случаях ее удается довести до конца, получив достаточно простые и удобные формулы для определения искомых линий. Здесь необходимы численные методы, с помощью которых каждую конкретную мировую линию мы можем с любой степенью точности вычислить постепенно, шаг за шагом. Так или иначе закон инерции в любой системе отсчета может быть сформулирован. Все, что нужно знать для этого, это формулу собственного времени. Так же обстоит дело и с другими законами физики. Каждый из них допускает формулировку, применимую в совершенно произвольной системе отсчета. И опять-таки для этого о самой системе отсчета нужно знать лишь, как в ней выражается через координаты событий интервал собственного времени. Выражение интервала собственного времени полностью определяет все свойства системы отсчета. Так, если нам задана система отсчета, о которой известно лишь, что в ней собственное время выражается формулой
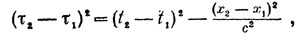 |
то мы сразу можем сказать, что эта система инерциальная и, следовательно, к ней применимы все наши прежние выводы: закон сложения скоростей, формула зависимости релятивистской массы от скорости, формулы для импульса и энергии и т. д. В неинерциальных системах отсчета все эти формулы будут иметь, вообще говоря, другой вид. Так, например, в нашей «равноускоренной» системе отсчета формула для релятивистской массы будет такой:
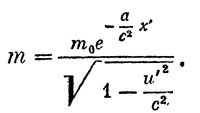 |
Мало того. Физические законы можно сформулировать не только в каждой конкретной системе отсчета. Можно заранее придать им такую форму, что они оказываются справедливыми автоматически в любой системе отсчета. Для закона инерции такую формулировку мы уже знаем. Требование максимальности интервала собственного времени относится к любой системе отсчета, как инерциальной, так и неинерциальной. Аналогичным образом обстоит дело и с другими законами (второй закон Ньютона, законы электромагнитного поля и т. д,). Можно даже указать ряд общих правил, на основании которых тот или иной физический закон, выведенный лишь в инерциальных системах отсчета, можно выразить в форме, пригодной уже для произвольных систем (или, как говорят, в общековариантной форме).
Это обстоятельство, свидетельствующее о большом успехе математической физики, дало повод некоторым авторам к ряду, выражаясь мягко, легкомысленных высказываний. Так, сам Эйнштейн в своей известной популярной книге «Эволюция физики» (написанной им совместно с польским физиком Инфельдом) говорит, что возможность такой формулировки физических законов означает полное равноправие всех мыслимых систем отсчета, в том числе и систем Птолемея и Коперника. Тем самым вся жестокая борьба, которая в свое время шла между сторонниками этих двух систем и в которой такие мыслители, как Джордано Бруно, поплатились жизнью — объявляется лишенной смысла. Система Коперника не правильнее, она просто удобнее, так как в ней движение планет описывается наиболее простыми математическими формулами.
Неудивительно, что подобного рода высказывания встретили резкий отпор как со стороны советских, так и со стороны ряда зарубежных ученых. Объявить на основании формального равноправия всех систем отсчета бессмысленным великое открытие Коперника — значит допустить совершенно непозволительную передержку, значит полностью игнорировать не только историю науки, но и реальную физическую сущность вопроса.
Разберем этот вопрос подробнее. Верно ли, что система Коперника проще всех других систем отсчета? Ясно прежде всего, что простота, удобство — понятия в высшей степени субъективные; вводить столь расплывчатые критерии в точную науку по меньшей мере рискованно. Кроме того, система Коперника, вообще говоря, не так уже проста. Движение планет в этой системе подчиняется сравнительно несложным закономерностям лишь при условии, что мы не учитываем влияния их друг на друга. Расчет же точного движения планет — дело весьма и весьма нелегкое; например, наиболее полная формула движения Луны занимает десятки страниц. Здесь вся пресловутая простота системы отсчета буквально тонет среди невообразимого множества различных факторов, влияющих на движение планет. В какой-нибудь другой системе отсчета эти формулы выглядели бы не намного сложнее.
Преимущества системы отсчета Коперника заключаются не в ее простоте, хотя — слов нет — эта простота является весьма сильным аргументом. Причины, выделяющие эту систему из числа других мыслимых систем отсчета, заключены гораздо глубже. Как мы только что заметили, система Коперника проста лишь при условии, что мы отвлекаемся от взаимного влияния планет друг на друга. Но это означает, что из множества всех действующих на планеты сил мы выделяем одну-единственную — силу тяготения Солнца. Именно эта сила является главной, именно она определяет общую структуру солнечной системы. И именно система Коперника позволяет выделить эту силу в наиболее чистом виде, освободить ее от всяких посторонних и случайных прибавлений. Для того чтобы объяснить на основании общих физических законов движение планет в системе отсчета, связанной, например, с Землей, нам пришлось бы, кроме силы тяготения, ввести в рассмотрение также центробежную силу инерции, возникающую вследствие вращения этой системы отсчета. Такая сила носит случайный характер, она не только не помогает нам разобраться в законах, управляющих движением небесных светил, но, наоборот, способна только излишне замаскировать их.
Таким образом, система Коперника лучше всего соответствует физической структуре солнечной системы. Будь эта структура другой (например, если бы Юпитер имел массу, приближающуюся к массе Солнца), система Коперника потеряла бы всякий смысл. И именно в силу этого соответствия законы движения планет выглядят в ней всего проще. После открытия Коперника сразу стало ясно, что человеческому разуму вполне под силу отыскать единые закономерности, управляющие движением планет; ученые стали их искать и, как мы хорошо знаем, эти поиски были блестяще завершены Кеплером. А математический анализ законов Кеплера привел Ньютона к открытию всемирного тяготения, В системе же Птолемея движение планет имеет столь запутанный характер, что отыскать тут один общий закон, которому подчиняется вся солнечная система,— дело почти безнадежное. Стало быть, центр системы отсчета нужно совместить с Солнцем потому, что Солнце является физическим центром своей системы. Если мы мысленно удалим из солнечной системы Землю, то на движении остальных планет такая операция почти не скажется; удалив же Солнце, мы тем самым изменим всю солнечную систему самым радикальным образом.
Система Коперника обладает еще тем существенным преимуществом, что она инерциальна — с огромной степенью точности можно считать, что Солнце движется равномерно и прямолинейно. Но эта особенность системы Коперника, выдвигаемая на первый план очень многими физиками, в данном вопросе играет второстепенную роль. В самом деле, вообразим на минуту, что Солнце имеет заметный электрический заряд, а в области пространства, занимаемой солнечной системой, существует достаточно сильное внешнее электрическое поле. Тогда, очевидно, Солнце будет двигаться ускоренно, увлекая за собой все планеты; связанная с ним система отсчета уже не будет инерциальной. Но все же именно эта система и никакая другая окажется, конечно, наиболее подходящей для изучения структуры солнечной системы.
С другой стороны, не следует и чрезмерно преувеличивать роль системы Коперника. Всякая система отсчета сама по себе есть не более чем система описания физических явлений. Какое-либо физическое содержание она может получить только за счет свойств той физической системы, которую она описывает. Для изучения движения Луны, например, во многих отношениях удобна система отсчета, связанная с Землей; система Коперника бесполезна и для исследования структуры всей нашей Галактики в целом. Астрономы пользуются многими системами координат, в том числе и экваториальной, в которой Земля не только не движется поступательно, но и не вращается.
В связи со всем сказанным уместно вспомнить, что еще за 125 лет до создания общей теории относительности французский математик Лагранж сумел сформулировать законы классической механики в столь общей форме, что она оказалась пригодной для любых, инерциальных и неинерциальных, систем отсчета. Однако Лагранж воздержался от высказываний о равноправии систем Коперника и Птолемея, хотя оснований к этому у него было не меньше, чем у Эйнштейна. Нужно заметить, что исследования Лагранжа и других работавших в том же направлении ученых сыграли очень большую роль в развитии теоретической физики.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Выберем на чертеже (рис. 30) оси x и ct для системы отсчета S. Нанесем на этот чертеж мировую линию нашей ракеты. Из § 12 мы знаем, что это будет гипербола, асимптоты которой пересекаются в точке Р (см. рис. 26). Мы будем рассматривать эту гиперболу целиком, считая, что ракета двигалась равноускоренно и до момента, который мы выбрали в качестве начала отсчета времени; в это время она, очевидно, двигалась справа налево. В точке О ракета на мгновенье останавливается, а затем движется в обратную сторону.
Выберем на чертеже (рис. 30) оси x и ct для системы отсчета S. Нанесем на этот чертеж мировую линию нашей ракеты. Из § 12 мы знаем, что это будет гипербола, асимптоты которой пересекаются в точке Р (см. рис. 26). Мы будем рассматривать эту гиперболу целиком, считая, что ракета двигалась равноускоренно и до момента, который мы выбрали в качестве начала отсчета времени; в это время она, очевидно, двигалась справа налево. В точке О ракета на мгновенье останавливается, а затем движется в обратную сторону.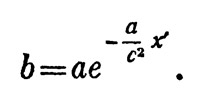


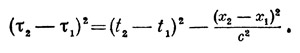

 Пусть даны две мировые точки А и В. Соединим их отрезком какой-нибудь мировой линии (рис. 35), Вычислим вдоль этого отрезка интервал собственного времени. Для этого мы можем воспользоваться любой системой отсчета — результат от этого зависеть не будет. Но от самой мировой линии результат зависит: взяв другую линию, получим другой интервал. Среди всевозможных линий, соединяющих точки А и В, существует одна-единственная, для которой соответствующий интервал собственного времени принимает наибольшее возможное значение. Это будет мировая линия тела, которое движется по инерции. Как ее найти? В инерци-альной системе отсчета задача решается исключительно просто — эта линия будет прямой. Но отыскать ее можно и в любой другой системе отсчета. Решением подобных задач о нахождении линий, для которых определенная величина принимает наибольшее или наименьшее значение, занимается особая математическая дисциплина — вариационное исчисление. Воспользовавшись методами вариационного исчисления, мы и найдем мировую линию тела, двигающегося по инерции.
Пусть даны две мировые точки А и В. Соединим их отрезком какой-нибудь мировой линии (рис. 35), Вычислим вдоль этого отрезка интервал собственного времени. Для этого мы можем воспользоваться любой системой отсчета — результат от этого зависеть не будет. Но от самой мировой линии результат зависит: взяв другую линию, получим другой интервал. Среди всевозможных линий, соединяющих точки А и В, существует одна-единственная, для которой соответствующий интервал собственного времени принимает наибольшее возможное значение. Это будет мировая линия тела, которое движется по инерции. Как ее найти? В инерци-альной системе отсчета задача решается исключительно просто — эта линия будет прямой. Но отыскать ее можно и в любой другой системе отсчета. Решением подобных задач о нахождении линий, для которых определенная величина принимает наибольшее или наименьшее значение, занимается особая математическая дисциплина — вариационное исчисление. Воспользовавшись методами вариационного исчисления, мы и найдем мировую линию тела, двигающегося по инерции.