Главная >> Введение в теорию относительности

§ 1. Аксиоматический метод в математике и физике

Одним из самых замечательных памятников древнегреческой науки являются знаменитые «Начала» Евклида. В этом выдающемся математическом сочинении не только собраны все основные геометрические знания, которыми владели греческие математики в третьем веке до нашей эры, но и сделана первая успешная попытка изложить геометрические факты в строгой логической последовательности. Книга открывается определениями и аксиомами, после чего все колоссальное здание геометрии строится на основе этих аксиом уже чисто логическим, дедуктивным путем. Каждое геометрическое предложение, даже если оно вполне «очевидно», строго доказывается. Впервые со всей возможной в то время полнотой в книге выступает аксиоматический метод, ставший для современной математики обязательным.
 
Не все, конечно, в книге Евклида было гладко. Не все доказательства оказались безупречными. Система аксиом была не совсем полной, т.е. в своих доказательствах Евклид опирался подчас на не высказанные явно, казавшиеся ему самоочевидными, предложения. С другой стороны, некоторые аксиомы оказались излишними — они, как позднее обнаружилось, вытекали из других аксиом.
 
Долгое время математики занимались «чисткой» сочинения Евклида, исправляя отдельные доказательства, формулируя недостающие аксиомы, заменяя одни аксиомы другими,  более удачно сформулированными,  и исключая лишние аксиомы. В особенности много попыток было сделано для того, чтобы исключить (т. е. доказать знаменитый пятый постулат) Евклида.
 
Этот постулат эквивалентен всем известному утверждению, что через каждую точку, не лежащую на данной прямой, проходит единственная прямая, ей параллельная. Многим математикам это высказывание представлялось менее очевидным, чем остальные аксиомы, и они приложили немало усилий, чтобы вывести его из других аксиом. Задача, однако, оказалась чрезвычайно трудной. Все попытки неизменно кончались неудачей. Даже выдающиеся математики попадали здесь впросак — им казалось, что они, наконец, нашли искомое доказательство, но проходило время, в этом доказательстве обнаруживалась та или иная ошибка, и дело оканчивалось полным конфузом. Ныне некоторые из этих «доказательств» демонстрируются студентам с назидательной целью, в виде примеров того, какую тщательность должен проявлять в своих исследованиях каждый математик.
 
Время шло; наука не стояла на месте. Были заложены основы аналитической геометрии. Ньютон и Лейбниц создали дифференциальное и интегральное исчисление. А пятый постулат все еще был бревном в глазу у геометров. Постепенно вокруг попыток его доказательства образовался целый своеобразный раздел геометрии. Было совершенно строго доказано, что хоть одна параллельная заведомо существует. Дело оставалось за «малостью» — доказать, что такая прямая может быть только одна. Было открыто много предложений, эквивалентных пятому постулату (одно из них состоит, между прочим, в том, что сумма всех углов треугольника равна двум прямым углам).
 
Надо сказать, что основным методом «доказательства» пятого постулата было доказательство от противного. Предполагали, что через точку вне прямой может проходить несколько ей параллельных, и старались прийти к противоречию. Для этого, естественно, нужно было извлекать различные формальные следствия из нового постулата (и остальных аксиом). Понятно, что эти следствия выглядели подчас довольно парадоксально (получалось, например, что сумма углов треугольника зависит от его площади), но математики не особенно об этом задумывались — им важно было получить два таких следствия, которые противоречили бы друг другу. Тем самым злосчастный постулат был бы доказан от противного. Но несмотря на всю необычность, а подчас и почти нелепость полученных на этом пути теорем, логического противоречия никак не получалось.
 
И вот, наконец, наиболее прозорливые математические умы стали приходить к мысли, что противоречия так и не будет, что пятый постулат Евклида доказать невозможно. К такому убеждению пришли наш великий соотечественник Лобачевский и почти одновременно с ним немецкий математик Гаусс и венгерский математик Больяй. И вот тогда-то перед изумленными взорами математиков стала открываться новая, неизведанная «страна» — неевклидова геометрия.

В самом деле, что значит, что пятый постулат нельзя доказать от противного? Очевидно, одно — он не противоречит остальным аксиомам. И если извлекать из него все новые и новые следствия, получится ни много, пи мало, как новая геометрия. Сколь необычно она ни выглядела, она оказывалась свободной от противоречий. А все теоремы, накопленные в течение многовековых попыток доказательства постулата Евклида, суть не что иное, как составные части новой геометрии.
 
  Большинство математиков того времени склонно было рассматривать эту «воображаемую» геометрию как некий курьез, как странную и, пожалуй, забавную игру понятий. Почти никто не придавал сколько-нибудь серьезного значения открытию Лобачевского. В этом нет ничего удивительного. В то время здание геометрии казалось незыблемым, ее аксиомы — непреложными истинами. Нашлись даже философы, объявившие геометрические аксиомы предпосылками правильного мышления, данными человеку от рождения, от природы. Тем самым всякая новая геометрия заранее объявлялась ересью.

Но сам Лобачевский сумел правильно понять значение новой геометрии. Он рассуждал так: в математике  налицо две геометрии. Спрашивается, какая же из них действует в окружающем нас мире? Все мы уверены, что евклидова. Но откуда, собственно, взялась эта уверенность? Конечно, из опыта, из практики. Применяя на практике теоремы евклидовой геометрии, мы неизменно приходим к правильным результатам. Но ведь все наши измерения содержат неизбежные погрешности.  Откуда мы знаем, например, что сумма углов реально го треугольника равна двум прямым углам? Быть может, если применить особо совершенную измерительную технику, обнаружится, пусть крайне малое, но
 все же ощутимое рас хождение с этой теоремой? Лобачевский, как настоящий материалист, был убежден, что толь ко опыт может решить вопрос, какая же геометрия больше отвечает действительности. Тем самым проблема геометрии реального мира переходит, собственно говоря, в область физики.
 
Забегая вперед, скажем, что Лобачевский был совершенно прав. Геометрия окружающего нас пространства не совсем евклидова. Правда, отклонения от евклидовой геометрии столь малы, что прямыми измерениями обнаружить их пока не удается, но мы знаем о них по косвенным признакам.

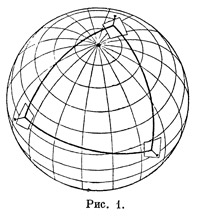
Впрочем, независимо от этого очень скоро было обнаружено, что неевклидовы геометрии (нетрудно понять, что их можно построить много) имеют вполне реальный смысл. Чтобы в этом убедиться, достаточно проделать следующий простой опыт. Возьмем глобус и приколем к нему булавками в трех не очень близких между собой точках три кусочка бумаги (рис. 1). Затем между этими булавками натянем три нитки, так что образуется треугольник. Срисуем карандашом углы треугольника на бумажки, снимем булавки и вырежем начерченные углы. Приложив их друг к другу, мы убедимся, что их сумма будет больше двух прямых. Таким образом, на поверхности сферы царит совсем не евклидова геометрия.

Читатель может возразить, что геометрия эта не совсем «настоящая», что по поверхности шара нельзя
 проводить прямые, что наш «треугольник», собственно, даже и не треугольник, а криволинейная фигура, и т.д. Но речь идет именно о внутренней геометрии сферической поверхности. Ясно, что на этой поверхности нельзя провести прямую. Однако роль прямых здесь с успехом могут играть линии, обозначаемые натянутыми нитями. И тот хорошо известный факт, что любая карта земной поверхности содержит неизбежные искажения   оригинала, связан как  раз  с неевклидовым характером внутренней геометрии сферической поверхности.
 
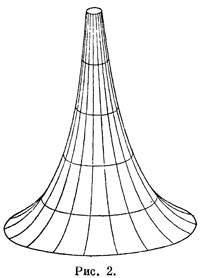
Мы можем повторить наш опыт с другой поверхностью, например с цилиндрической. Тут мы обнаружим, что сумма углов треугольника равна в точности двум прямым углам, несмотря на то, что и этот треугольник не «настоящий». Значит, дело здесь совсем не в том, что наши поверхности кривые, а именно в характере их внутренней геометрии. Каждая поверхность имеет свою геометрию. В частности, существует поверхность, на которой действует как раз геометрия Лобачевского; она называется псевдосферой, хоть на сферу она и не похожа (рис. 2). Кстати, существование такой поверхности служит отличным доказательством непротиворечивости геометрии Лобачевского, а стало быть, и невозможности доказательства пятого постулата Евклида.
 
Теория таких внутренних геометрий получила в математике большое развитие. Основываясь как на результатах исследований Лобачевского, так и на этой теории, немецкий математик Риман разработал общие принципы построения различных геометрий, объединив их все в единую теорию, которая получила название римановой геометрии. Риман подтвердил также мысль Лобачевского о том, что геометрия реального мира есть вопрос физический.
 
Физикам суждено было столкнуться с этим кругом математических идей сначала в несколько иной плоскости. По мере развития науки математика все глубже проникала в физику. Характерным примером здесь может служить то, что один из творцов дифференциального и интегрального исчисления — Исаак Ньютон — являлся в то же время крупнейшим физиком-теоретиком. Весьма существенно, что математика проникала в физику не только в качестве аппарата для формальных выкладок и вычислений — она несла с собой и свои идеи. Такой идеей был, в частности, аксиоматический метод.
 
Ньютон хорошо понимал, что для строгого и безупречного построения физической науки аксиоматический метод является наиболее подходящим средством. Ему принадлежит заслуга выделения из всего огромного многообразия физических фактов и закономерностей тех основных, фундаментальных законов, на которых можно было бы построить все здание физики. Ньютон вполне последовательно назвал эти законы аксиомами движения (между прочим, основной его труд тоже носил название «Начал» — точнее, «Математические начала натуральной философии», т. е. физики). Эти основные законы Ньютона известны ныне каждому школьнику. Ньютон попытался — и не без успеха — построить механику, подобно Евклиду, чисто дедуктивным путем, основываясь исключительно на сформулированных им аксиомах. Те пробелы и недостатки, которые мы теперь находим в рассуждениях Ньютона, нисколько не умаляют его научного подвига.

Весьма замечательно, что история, подобная открытию неевклидовой геометрии, разыгралась и в физике; здесь она носила, пожалуй, еще более драматический характер. Она произошла в первое десятилетие нашего века и связана главным образом с именем великого немецкого физика Альберта Эйнштейна.

СМОТРИТЕ ТАКЖЕ: