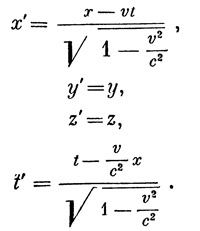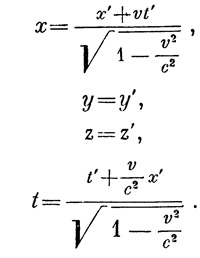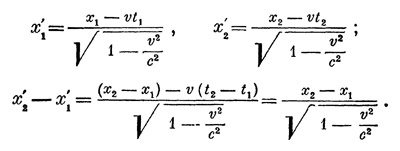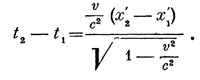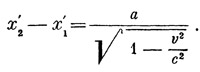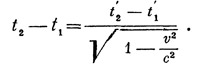Главная >> Введение в теорию относительности § 8. Преобразования Лоренца
До сих пор мы занимались лишь решением отдельных простейших задач теории относительности. Теперь мы познакомимся с формулами гораздо более общего характера, которые позволят получить целый ряд важных и интересных следствий. Но сначала нам нужно уточнить некоторые понятия.
Мы все время говорили о двух наблюдателях, один из которых неподвижен, а другой едет в поезде. Наблюдая одни и те же события, они приходят к разным выводам. Понятие «наблюдателя», как уже отмечалось, несмотря на известную наглядность, вносит во. все выводы теории некоторый оттенок субъективности, создает иногда впечатление, что эти выводы зависят от того, что «кажется» какому-то наблюдателю. В действительности теория относительности вообще не имеет дела ни с какими «наблюдателями». Вместо них имеется понятие системы отсчета.
Под системой отсчета понимается всякий прибор или комплекс приборов и устройств, работающих совместно и способных фиксировать место и время каждого события. При этом совершенно безразлично, управляются ли эти приборы человеком, или они работают автоматически.
Полвека назад, во времена создания теории относительности, классической моделью системы отсчета был набор твердых стержней для измерения расстояний и часы для отсчета времени. Теперь, когда техника шагнула вперед, мы можем применить и другие, более современные модели. Так, весьма удобна и наглядна модель системы отсчета в виде радиолокационной станции. Надо думать, что с принципами радиолокации читатель знаком, хотя бы в самых общих чертах. Для установления местонахождения того или иного объекта (например, самолета) со станции посылается радиоимпульс, который, отразившись от этого объекта, возвращается обратно. Телевизионная техника позволяет с достаточной точностью измерить промежуток времени между отправлением сигнала и его возвращением. А так как скорость сигнала известна — она равна скорости света,— то отсюда непосредственно получается и расстояние до исследуемого объекта. Зная же расстояние до момента события и направление на него, мы определим тем самым его точные координаты. Время фиксации объекта также легко вычисляется, ибо скорость сигнала в обе стороны одинакова. Следует признать, что такая система отсчета во многих отношениях удобнее старых громоздких систем из твердых стержней, и мы бы советовали читателю к ней привыкнуть. К тому же само понятие абсолютно твердого тела в теории относительности, как уже отмечалось, не вполне корректно.
Но дело, конечно, не в конкретной «конструкции» системы отсчета. В своих исследованиях физики пользуются самыми различными приборами для измерения длин и промежутков времени, выбирая их из соображений точности, удобства и простоты. Какими бы приборами ни регистрировать события, в пределах определенной для каждого прибора степени точности каждый из них даст одни и те же показания. Поэтому мы не будем уточнять вопрос о конкретизации системы отсчета, если это не будет вызываться стремлением к особой наглядности.
Весьма существенным является предположение о возможности приписать всей системе отсчета в целом определенную скорость по отношению к любому телу или другой системе отсчета.
Теперь мы вместо выражений «скорость тела с точки зрения данного наблюдателя» или «время события для данного наблюдателя» будем говорить: «скорость тела в данной системе отсчета» и «время события в данной системе отсчета». Различные системы отсчета могут давать при этом различные результаты; одной из основных задач теории относительности является установление связи между ними. Другой важной задачей является изучение тех свойств явлений, которые не зависят от выбора той или иной системы отсчета.
Окружающее нас пространство имеет три измерения. Это значит, что для указания места любого события необходимо задать три числа. Эти три числа связаны с некоторой системой координат, которая вводится в пространство с помощью той же системы отсчета. Для теоретических исследований часто привлекаются прямоугольные декартовы координаты, которые во многих отношениях проще и удобнее других координатных систем. Но вполне возможны и другие координатные системы,— например, астрономы для указания точного места светила указывают его прямое восхождение, склонение и расстояние от Земли.
Но для полного указания события трех координат недостаточно, необходимо еще задать момент времени, в который происходит событие. Таким образом, событие определяется четырьмя числами. В этом смысле можно сказать, что пространство событий имеет четыре измерения. Здесь нет, конечно, никакой мистики — пространственных координат по-прежнему остается три; четвертая координата — временная — качественно отличается от пространственных. Объединение четырех координат события в единый комплекс объясняется отнюдь не стремлением стереть всякую разницу между пространством и временем. По пространству можно, например, двигаться взад и вперед, но никакая теория относительности не дает возможности построить «машину времени», на которой можно было бы отправиться в каменный век.
Иногда можно услышать вопрос: а почему, собственно, четырехмерный мир составляет привилегию теории относительности? Ведь тот факт, что для указания события нужно не три, а четыре числа, не есть какое-то великое открытие. По существу, четыре координаты нужны были для этого испокон веков. Почему же Ньютон мог обходиться трехмерным миром, а Эйнштейну понадобился мир четырехмерный? На этот вопрос мы ответим немного позднее.
Нашей задачей является сейчас установление связи между координатами одного и того же события в двух различных системах отсчета. Пусть имеются две системы отсчета S и S`, удовлетворяющие следующим условиям:
1. В обеих системах пространственные координаты суть прямоугольные декартовы координаты. Мы будем обозначать их соответственно через х, у, z и х`, у`, z`
 |
2. Система отсчета S` движется относительно системы отсчета S прямолинейно и равномерно со скоростью v. Очевидно, что система S движется относительно системы S` со скоростью —v.
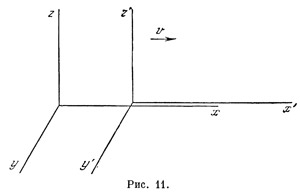
3. Координатные оси х и х` направлены по движению и скользят одна по другой; оси y, z и у`, z` соответственно параллельны (рис. 11).
4. В момент времени t=t` =0 начала координат в обеих системах отсчета совпадают, т. е. событие, все четыре координаты которого равны нулю в одной системе, имеет в другой системе также нулевые координаты.
Оказывается, что при этих условиях координаты одного и того же события в обеих системах связаны следующими формулами:
Эти формулы позволяют рассчитать координаты х`, у`, z`, t` некоторого события в системе S`, если известны его координаты х, y, z, t в системе S. Обратный переход от системы S` к системе S дается формулами
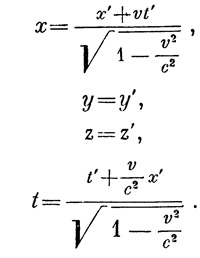 |
Эти формулы носят название формул преобразований Лоренца, так как они были впервые получены Лоренцом; эти формулы и выражают тот особый принцип относительности, которому удовлетворяют уравнения Максвелла. Теория относительности оставила их без изменения, придав им новый смысл.
Рассматривая эти формулы, мы прежде всего замечаем, что координаты у, z не преобразовываются; это отвечает отсутствию поперечного лоренцова сокращения. Далее, формулы преобразований в ту и другую сторону совершенно симметричны, лишь скорость v заменена на —v. Это, конечно, отвечает факту равноправия всех систем отсчета. Самое же главное, преобразуется не только пространственная координата х, но и время t. Это означает, как мы уже знаем, относительность не только пространственных координат, но и времени. Можно заметить, что формулы для преобразования времени очень похожи на формулы для преобразования пространственной координаты х; это сходство еще больше можно усилить, если вместо величины t ввести величину ct. Формулы тогда станут совершенно симметричными. Формально, таким образом, время ничем не отличается от пространственных координат.
Интересно сравнить преобразования Лоренца с «классическими» нерелятивистскими формулами преобразования от одной системы отсчета к другой. Во-первых, в ньютоновской механике время не преобразовывается, так что t=t`. Далее, если координаты некоторого события в системе S` суть х`, t` (двух других пространственных координат мы можем не рассматривать— они по-прежнему не меняются), то, поскольку система S` за промежуток времени vt` сдвинется относительно системы S на расстояние vt` получим x=x`+vt`. Таким образом, формулы
x=x`+vt`,
t = t`
и обратные им
x` = x - vt,
t` = t
играют в классической механике ту же роль, какую в механике релятивистской играют преобразования Лоренца. «Классические» формулы получили название формул преобразований Галилея. Нетрудно заметить, что когда скорость v относительного движения систем отсчета мала по сравнению со скоростью света, преобразования Лоренца дают практически тот же результат, что и преобразования Галилея. Так, конечно, и должно быть, и именно в этом смысле теория относительности никоим образом не отменяет классической механики. Преобразования Галилея можно формально получить из преобразований Лоренца, если считать величину с бесконечно большой. Напомним, что с — не только скорость света, но и максимальная скорость распространения взаимодействия («сигналов»). Это означает, что в классической физике в принципе допустимы любые, даже бесконечные скорости распространения взаимодействий. Об этом мы уже говорили подробно, когда обсуждали вопросы, связанные с «дальнодействием» и «близкодействием».
То обстоятельство, что при переходе от одной системы отсчета к другой время преобразуется так же, как и пространственные координаты, заставляет рассматривать все четыре координаты события как единое целое. Теория относительности устанавливает, таким образом, тесную связь между пространством и временем, связь, которой в классической физике не существовало. Эта связь проходит красной нитью через всю теорию относительности и влечет за собой объединение в единый комплекс других, ранее представлявшихся совершенно независимыми понятий, например энергии и количества движения. В этом состоит одна из самых замечательных особенностей теории относительности.
Следует заметить, что столь же четко проводится через всю теорию идея об отличии пространства от времени. Ни преобразованиями Лоренца, ни какими-либо другими преобразованиями, допустимыми в теории относительности, нельзя превратить пространство во время или наоборот. Качественная разница между этими понятиями никогда не стирается.
Теперь мы можем ответить на вопрос, почему «четырехмерный мир» вошел в физику вместе с теорией относительности. В классической физике время никогда не менялось, оно было одним и тем же во всех системах отсчета. Поэтому объединение в единый комплекс всех четырех координат события было бы просто механической операцией, никому, в сущности, не нужной, ибо одна из координат — временная — никогда не изменялась. Четырехмерное пространство—время распадалось бы все равно на свой составные части — трехмерное пространство и одномерное время.
Иное дело — механика релятивистская. Здесь время при переходе от одной системы отсчета к другой преобразуется вместе с пространственными координатами, в этом отношении ничем среди них не выделяясь. «Четырехмерный мир» теперь уже не распадается. Поэтому теперь был бы искусственным, наоборот, отрыв временной координаты от пространственных. Все четыре координаты события должны рассматриваться вместе как единое целое.
Заметим еще, что в первых работах Эйнштейна «четырехмерный мир» еще не фигурировал. Он был введен через три года немецким математиком Минковским и с тех пор стал неотъемлемой частью теории относительности. Поэтому «четырехмерный мир» называют часто пространством Минковского.
Мы не будем приводить здесь вывод формул преобразований Лоренца, хоть для этого и располагаем уже всеми необходимыми средствами. Ограничимся лишь проверкой того, что из формул преобразований Лоренца непосредственно вытекают все ранее полученные результаты. Для упрощения выкладок мы не будем рассматривать пространственные координаты у и z. Это вполне законно, так как во всех рассмотренных нами ранее «мысленных экспериментах» события разыгрывались лишь вдоль некоторого прямого железнодорожного пути. Для задания места такого события вполне достаточно одного числа, например расстояния от какой-нибудь станции. Можно сказать, что пространство у нас было, по существу, одномерным, а «мир», т. е. пространство — время, — двумерным.
Следует подчеркнуть, что в формулы преобразований Лоренца входят не длины отрезков и не промежутки времени, а координаты отдельных событий. Поэтому при переводе какого-либо явления с «языка» одной системы отсчета на «язык» другой необходимо сначала картину этого явления изложить на «языке» событий. Например, чтобы определить длину какого-либо тела, нужно рассмотреть два события, совершающихся на его концах и совершающихся одновременно (в данной системе отсчета). Тогда разность пространственных координат этих событий и даст искомую длину.
Перейдем к рассмотрению уже известных нам релятивистских эффектов.
1. Формула лоренцова сокращения. Пусть имеется твердый стержень, покоящийся в системе S`. Обозначим пространственные координаты его концов в этой системе через х`1 и x`2. Длина его (в
системе S`) равна, очевидно, х`2 - x`1. Чтобы измерить его длину в системе S, нужно рассмотреть два события, совершающихся одновременно на его концах. Пусть их координаты суть x`1,t и х`2, t2; по условию t1=t2. Тогда из формулы, выражающей х через х и t, получаем
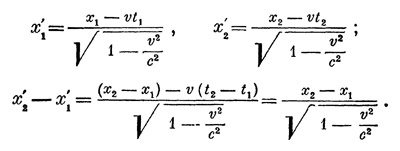 |
Это и есть формула лоренцова сокращения.
2. Относительность одновременности. Пусть в системе отсчета S` («поезде») происходят два одновременных события с координатами x`1,t` и x`2,t`. Вычислим разность их временных координат в системе S («с точки зрения неподвижного наблюдателя»). Из формулы, выражающей t через t` и х`, легко получаем
Эта формула отличается от той, которая была получена нами в § 5, так как там фигурировала длина а поезда в системе отсчета S («для земного наблюдателя»), тогда как теперь в формулу входит разность координат х`2 и x`1, равная длине поезда в системе S`. Чтобы получить полное совпадение формул, достаточно использовать формулу лоренцова сокращения
После подстановки убеждаемся, что мы пришли к старому результату. Заметим, что вместо а было бы неправильно писать х2 — x1, так как рассматриваемые события в системе S неодновременны, а потому х2 — х1 ≠ а.
3. Замедление времени. Пусть в системе отсчета S` («поезде») происходят два события в одной
и той же точке, так что их координаты суть х`, t`1, и х`,t`2. Промежуток Бремени между этими событиями в системе S` есть, очевидно, t`2 — t`1. Вычислим тот же промежуток в системе отсчета S («для неподвижного наблюдателя»). Из той же формулы, что и ранее, получаем
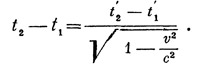 |
Читатель без труда убедится, что и это — старый наш результат.
Итак, из формул преобразований Лоренца следуют все рассмотренные нами «эффекты». В дальнейшем мы получим из них еще целый ряд следствий. Преобразования Лоренца занимают в теории относительности весьма важное место, составляя одну из ее математических основ. Между прочим, анализ этих формул приводит к доказательству непротиворечивости теории относительности, так что все попытки получить из ее постулатов два противоречащих друг другу следствия заранее обречены на неудачу.
В заключение заметим, что формулы преобразований Лоренца теряют смысл, если v=c, так как тогда в их знаменателях появляются нули, а деление на нуль, как известно, невозможно. Это значит, что никакие две системы отсчета не могут иметь относительной скорости, равной скорости света. Отсюда вытекает, что и никакое материальное тело не может достичь скорости света, так как ко всякому телу можно «привязать» систему отсчета. Этот же результат следует и из других формул, например из формулы лоренцова сокращения: движущееся со скоростью света тело имело бы продольные размеры, равные нулю, что явно нелепо. Невозможность движения со скоростью света в дальнейшем еще неоднократно подтвердится.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|