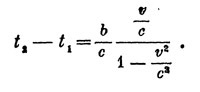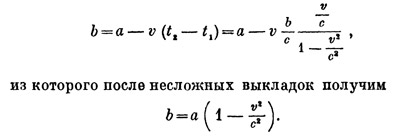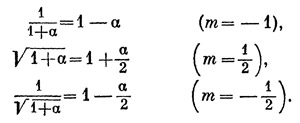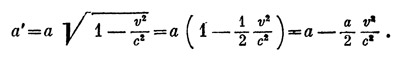Главная >> Введение в теорию относительности § 6. Лоренцово сокращение
Обратимся снова к нашему объекту исследования— движущемуся поезду. Попытаемся на этот раз «на ходу» измерить его длину. Для этого заранее установим в первом и последнем вагонах автоматические приборы, которые в определенный момент оставили бы на земле какие-то метки. Приборы отрегулируем так, чтобы они срабатывали одновременно с точки зрения сидящего в поезде наблюдателя.
Пусть поезд движется с какой-то определенной скоростью. Когда он проходит мимо нас, сидящий в нем наблюдатель нажимает кнопку, срабатывают приборы, и на земле появляются две отметки. Спрашивается, как по ним установить длину поезда?
Для едущего в поезде наблюдателя приборы сработали одновременно; поэтому расстояние между метками в точности равно длине поезда. Неподвижный же наблюдатель рассуждает иначе. Для него сработал сначала задний прибор, а потом — передний (см. начало § 5). За это время поезд успел несколько продвинуться. Поэтому расстояние между метками должно быть больше длины поезда.
Что же отсюда вытекает? Два отрезка, равные для одного наблюдателя, уже не равны для другого. Дело здесь, очевидно, в том, что эти отрезки движутся друг относительно друга. Мы говорим, что они равны, если их концы в какой-то момент совпадают. Но так как одновременность — понятие относительное, то и факт совпадения концов относителен.
Но отсюда вытекает также, что и длина отрезка — величина относительная, ибо в противном случае равенство или неравенство двух отрезков не зависело бы от наблюдателя. Значит, если два движущихся друг относительно друга наблюдателя измеряют один и тот же отрезок, они получат, вообще говоря, различные результаты. С другой стороны, если какое-либо тело меняет свою скорость, то для неподвижного наблюдателя будет меняться и его длина.
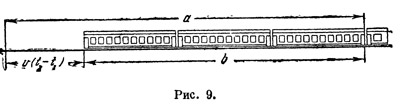
Прежде чем продолжать обсуждение этого вопроса, вычислим изменение длины движущегося отрезка, воспользовавшись для этого тем же поездом (рис. 9). Пусть Для неподвижного наблюдателя расстояние между оставленными поездом метками равно a, а длина поезда равна b. Оставляющие метки приборы срабатывают неодновременно; на основании результатов предыдущего параграфа мы можем утверждать, что разница во времени составляет
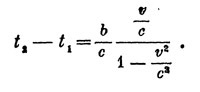
За это время поезд успеет Продвинуться на расстояние v (t2—t1). Чтобы получить его длину, нужно эту
величину вычесть из расстояния между метками. Мы приходим, таким образом, к уравнению
А теперь станем на точку зрения сидящего в поезде наблюдателя. Для него как поезд, так и расстояние между метками имеют другие длины. Обозначим поэтому теперь длину поезда через b` а расстояние между метками через а`. Так как с точки зрений движущегося наблюдателя эти длины совпадают, то а`= b`.
При переходе от движущегося наблюдателя к неподвижному поезд меняет свою длину — раньше она была равна b` а теперь равна b; допустим, что она изменилась при этом в k раз, так что b—kb`. Аналогично обстоит дело с длиной неподвижного отрезка — расстояния между метками — при обратном переходе от неподвижного наблюдателя к движущемуся. Так как, в силу принципа относительности, оба наблюдателя равноправны, длина этого отрезка должна измениться также в k раз, т. е. должно быть а` = ka.
Из отмеченного выше равенства а` =b` вытекает

Оба эти равенства означают, что движущийся отрезок «кажется» короче неподвижного. Этот релятивистский эффект получил название лоренцова сокращения.
Мы взяли слово «кажется» в кавычки потому, что речь у нас идет, конечно, не о том, что кажется тому или иному конкретному наблюдателю, а о том, что происходит на самом деле, независимо от какого бы то ни было наблюдателя. Во всех обсуждаемых нами мысленных экспериментах всегда можно заменить «наблюдателей» соответствующими приборами. Теория относительности — чисто физическая теория, и она не может заниматься вопросами особенностей восприятия явлений различными живыми «наблюдателями»; в дальнейшем мы вообще заменим «наблюдателей» более точным физическим понятием. Однако, ради большей наглядности, мы к «наблюдателям» будем прибегать и в дальнейшем, надеясь только что сделанной оговоркой избежать упреков в субъективизме и идеализме.
История происхождения названия лоренцово сокращение заслуживает внимания. Мы уже имели случай указать, что для объяснения результата опыта Майкельсона Лоренцом была высказана гипотеза о сокращении размеров всех тел при их движении сквозь эфир; предложенная им формула для этого сокращения формально совпадает с выведенной только что нами. Однако смысл этих двух формул совершенно различен.
У Лоренца эффект сокращения был эффектом динамическим в том смысле, что он объяснялся взаимодействием «элементарных» частиц, из которых построены все тела, с эфиром. Лоренц в своей электронной теории пришел к выводу, что движущийся электрон, испытывая воздействие со стороны эфира, должен «сплющиваться» в направлении движения, принимать вместо шарообразной некую линзообразную форму. Такому «сплющиванию», согласно Лоренцу, должны подвергаться вообще все тела. Таким образом, сокращение тел при их движении относительно эфира мог бы, в принципе, зафиксировать и движущийся вместе с этим телом наблюдатель. Беда в том, что такому же сокращению подвергаются также и все эталоны длины, так что в действительности это сокращение невозможно таким образом обнаружить. Далее, неподвижное тело имеет одну и ту же длину как для неподвижного, так и для движущегося наблюдателя; в этом смысле никакой относительности длины нет. Величина v, входящая в формулу лоренцова сокращения, означает скорость тела относительно эфира, а не скорость его относительно наблюдателя.
У Эйнштейна смысл той же формулы совсем иной. Никакого эфира не существует, поэтому и говорить о скорости относительно эфира бессмысленно. Движущиеся тела сокращают свои размеры не вследствие каких-то изменений, происходящих с ними самими, а просто потому, что они движутся относительно измерительного прибора. Этот эффект — не динамический, а чисто геометрический или, точнее, кинематический. Он стоит в одном ряду с такими привычными явлениями, как уменьшение угловой величины предмета при его удалении или «косой дождь».
Основной заслугой Эйнштейна было то, что он отказался от всяких попыток динамического объяснения лоренцова сокращения, усмотрев в этом явлении не результат взаимодействия тел с эфиром, а проявление свойств пространства и времени. Всякое материальное тело обладает определенными пространственными свойствами, которые мы обозначаем словами: длина, ширина, объем и т. д. Однако в физические уравнения и формулы входят не сами длины и объемы, а лишь измеряющие их числа. Числа эти отражают, конечно, соответствующие свойства исследуемого тела. Но ниоткуда не следует, что, например, число, измеряющее длину предмета, отражает только то его свойство, которое мы обозначаем словом «длина», и отражает его полностью, адекватно.
Раньше полагали, что, прикладывая к измеряемому предмету эталон длины, мы получаем число, полностью характеризующее только его длину. Теперь мы видим, что это число в определенной степени отражает также и состояние движения предмета относительно эталона.
Можно попытаться освободиться от такого «довеска», условившись раз навсегда измерять длину предмета только неподвижными относительно него эталонами. Часто (например, при измерении небесных или микроскопических тел) выполнить такое требование практически невозможно. Теория относительности указывает нам путь для преодоления этой трудности: нужно одновременно с длиной тела измерить его скорость и разделить длину на √(1 - v2/c2). Полученную величину можно назвать собственной длиной предмета; она, очевидно, не зависит от скорости тела или «наблюдателя», т. е. является величиной абсолютной.
Это напоминает астрономические определения размеров небесных тел. Чтобы найти, например, диаметр планеты, астрономы измеряют ее угловой («видимый») диаметр и одновременно расстояние до нее. Перемножив эти числа, получим «истинный» диаметр. Полученное число будет абсолютным в том смысле, что оно не зависит от расстояния до планеты: повторив эти измерения и вычисления в другой момент, когда расстояние до планеты будет другим, мы получим старый результат.
Понятно, что если говорить об индивидуальной характеристике пространственных свойств небесного тела, то его «истинный» диаметр является для этой цели более подходящей величиной, чем «видимый», который характеризует, кроме пространственных свойств тела, также и его отношение к другому телу — Земле. Точно так же и в теории относительности собственная длина есть индивидуальная характеристика тела. Относительная же «обыкновенная» длина характеризует также отношение данного тела к другому (например, к измерительному прибору).
Таким образом, в теории относительности единое «классическое» понятие длины тела как бы раздваивается на относительную длину и абсолютную собственную длину. Такое раздвоение понятий, как мы увидим, характерно для всей теории. Следует при этом иметь в виду, что относительные понятия играют ничуть не меньшую роль, чем абсолютные; именно относительные величины входят в важнейшие уравнения теории относительности, и когда говорят, например, о длине, то имеют в виду как раз относительную длину.
Возвращаясь к явлению лоренцова сокращения, подчеркнем еще раз, что оно, как и все релятивистские эффекты, имеет взаимный характер в силу относительности понятий движущийся и неподвижный. Пусть, например, наш поезд в неподвижном состоянии имеет длину ровно 1 км. Когда он начнет двигаться, неподвижный наблюдатель найдет, что его длина уменьшилась, так что будут моменты, когда поезд целиком помещается между двумя километровыми столбами. А для наблюдателя в поезде, наоборот, сократятся сами промежутки между столбами, так что будут моменты, когда два километровых столба будут помещаться между головой и хвостом поезда.
Как ни парадоксален этот факт, из него столь же невозможно извлечь противоречие, как и из факта относительности одновременности. И дело как раз в этой относительности. Действительно, что значит, что поезд целиком помещается между километровыми столбами? Это значит, что там находятся голова и хвост поезда одновременно с точки зрения неподвижного наблюдателя. А для движущегося наблюдателя эти события уже не одновременны; для него одновременны другие два события — когда два километровых столба помещаются между головой и хвостом поезда.
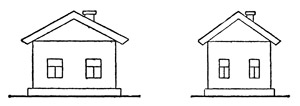 |
Мы до сих пор говорили о «продольном» лоренцовом сокращении, т. е. об изменении длины тела в направлении его движения. Можно показать, что поперечные размеры тела при этом не меняются. Таким образом, если мы укрепим неподвижно левый рисунок (рис. 10), а потом, двигаясь мимо него с достаточно большой скоростью, сделаем с него моментальный снимок, то получим нечто вроде того, что изображено на рис. 10 справа.
Для читателей, знакомых с фотографией, укажем на некоторую аналогию, существующую между лоренцовым сокращением и известным эффектом искажения снимков быстро движущихся предметов. Если для съемки применяется камера, снабженная шторно-щелевым затвором, то изображение объекта будет сжато или растянуто, в зависимости от направления движения шторки затвора. Это искажение вызвано тем, что изображение образуется лучами, попадающими на пленку в различные моменты времени.
Если теперь для такой же съемки применить камеру с центральным затвором, то, при условии достаточной величины скорости объекта, изображение будет искажено из-за лоренцова сокращения. Хотя теперь создающие изображение лучи проходят через объектив одновременно, но отражены от объекта они с точки зрения самого объекта неодновременно. Поэтому причины искажений в обоих случаях до некоторой степени аналогичны.
Можно заметить, что такая ситуация осуществляется при аэрофотосъемке, так что, обрабатывая полученные снимки, надо учитывать релятивистские искажения. Но, конечно, об этом можно говорить только в шутку, так как эти искажения лежат далеко за пределами точности современной измерительной техники. Чтобы убедиться в этом, вычислим лоренцово сокращение рассмотренной в предыдущем параграфе ракеты длиной 300 м, двигающейся со скоростью 10 000 км/час. Для этого в формулу
a` = a√(1 - v2/c2)
надо подставить а=300 м, с=300 000 км/сек, v = 10 000 км/час. Для облегчения подобного рода вычислений весьма полезна приближенная формула:
(1 + a)m = 1 + ma,
которая тем точнее, чем меньше а. Число m может быть любым — целым или дробным, положительным или отрицательным. В частности, давая ему конкретные числовые значения, мы получим ряд удобных приближенных формул, например:
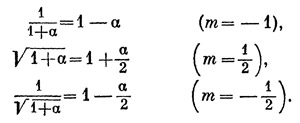
Погрешность этой формулы составляет примерно m(m—1)/2 * α2 , что в большинстве случаев для нас будет вполне достаточно. Конечно, если α не мало, формула может дать грубо искаженный результат, в чем читатель легко убедится, положив, например, α=1. В нашем случае приближенная формула дает
Величину v2/c2 мы уже вычисляли; она равна 0,840 * 10-10, так что приближенную формулу мы можем применить с полным правом. Теперь читатель легко подсчитает, что величина а` отличается от а на 1,26*10-8м = 12,6 миллимикрона. Малейшее изменение температуры даст гораздо больший эффект; ясно поэтому, что обнаружить и измерить лоренцово сокращение в таких условиях — задача безнадежная.
Однако читатель не должен делать вывод, что вообще все релятивистские эффекты имеют такой неуловимый характер. Очень скоро мы познакомимся с такими выводами теории относительности, которые могут быть проверены с большой степенью точности, а также с такими, которые буквально «бросаются в глаза».
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|