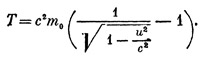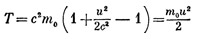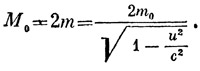Главная >> Введение в теорию относительности § 14. Масса и энергия
В предыдущем параграфе мы подробно выяснили понятие релятивистского импульса. Как помнит читатель, основой служили нам законы упругого удара. Но рассмотрения этих законов одновременно дает и формулу кинетической энергии; оказывается, что она имеет вид
Чтобы показать, что при малых скоростях она совпадает с классической, нужно воспользоваться все той же приближенной формулой. Тогда мы получим
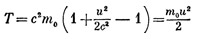 |
в полном согласии с ньютоновской механикой. Вспомнив формулу релятивистской массы, мы можем перевисать выражение для кинетической энергии в виде
Т=с2 (т — m0).
Значит, кинетическая энергия равна просто-напросто избытку массы тела над массой покоя, умноженному на квадрат скорости света.
То, что кинетическая энергия каким-то образом связана с релятивистской массой, не представляется удивительным, ведь с ростом скорости растет как масса, так и энергия. Но такое простое соотношение заставляет сделать далеко идущие выводы.
Для этого рассмотрим явление неупругого удара» Пусть два тела с одинаковыми массами покоя т0 движутся с равными скоростями и навстречу друг другу. Столкнувшись, они образуют новое тело с массой покоя Мо, которое будет неподвижно. Согласно закону сохранения массы, величина Мо будет равна сумме релятивистских масс обоих тел до столкновения
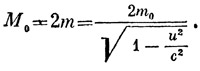 |
Масса покоя нового тела больше суммы масс покоя его составных частей. Кинетическая энергия до столкновения равна
Т = 2с2*(т — т0)=с2 (т0 — 2т0);
после столкновения кинетическая энергия равна нулю. Но кроме закона сохранения массы существует, как известно, закон сохранения энергии. Кинетическая энергия не пропала; она перешла в другой вид энергии (например, в тепло). Если мы через Ео обозначим суммарную внутреннюю энергию, частью которой является тепловая энергия обоих тел до столкновения, а внутреннюю энергию нового тела — через Е, то, очевидно,
E - E0 = T,
или
E - E0 = c2(M0 - 2m0).
Таким образом, приращение внутренней энергии оказывается равным приращению массы покоя, умноженному на с2.
Представим себе, что исходные два тела вначале были неподвижны; тогда общая масса системы этих тел была равна 2m0. Потом под действием каких-то сил они были разогнаны до скорости u. При этом им была сообщена энергия T, а масса их возросла до величины Мо. После столкновения масса и энергия остались прежними, лишь энергия испытала дальнейшее превращение. В итоге мы имеем, что суммарная масса рассматриваемой системы возросла на величину М0— 2m0, а общая энергия — на величину Е—Е0=с2(М0— 2m0).
Сообщавшие энергию первоначальным телам силы могут быть любой природы — упругие, электрические и т. д. В момент столкновения кинетическая энергия может переходить не только в тепловую; она может частью перейти, например, в электромагнитную энергию. Мы неизбежно приходим к заключению, что если системе тел (или полей) сообщена энергия Е любой природы, то масса этой системы возрастает на величину
M = E/c2.
Эйнштейн сделал следующий шаг. Он высказал утверждение, что полная внутренняя энергия любой физической системы равна ее массе, умноженной на квадрат скорости света:
E = c2m
Это значит, например, что полное количество энергии, заключенное в одном грамме вещества любой природы, равно примерно 25 миллионам киловатт-часов. Крупнейшая в мире Куйбышевская гидроэлектростанция вырабатывает такое количество энергии примерно за полсуток; этой энергии хватило бы, чтобы двигать автомобиль мощностью в 70 лошадиных сил непрерывно в течение пятидесяти лет.
То, что увеличение тепловой энергии ведет к увеличению массы, нас не должно удивить — ведь масса тела складывается из релятивистских масс молекул. При нагревании скорости молекул растут, откуда непосредственно вытекает, что и масса тела должна увеличиваться. Нетрудно подсчитать, что при нагревании тонны воды от 0 до 100° вес ее возрастает на 0,0000047мг. Солнце ежесекундно излучает количество энергии, которому соответствует потеря массы в 4 миллиона 200 тысяч тонн; это составляет примерно 1/2 000 000 000 000 000 000 000 долю общей солнечной массы. Из этого потока энергии на долю Земли достается «всего лишь» 1,2 кг. Можно добавить, что большая часть этой энергии отражается и рассеивается в мировом пространстве.
Эти примеры достаточно ясно показывают, как ничтожно мало «весит» энергия. Эйнштейн, придя к выводу о связи энергии с массой, не мог в то время указать ни одного эксперимента, который мог бы послужить надежным средством проверки этого заключения. В то же время он заметил, что соотношение Е=тс2, быть может, удастся проверить при исследовании процессов радиоактивности. Это указание оказалось прямо-таки пророческим: в настоящее время формула Эйнштейна играет основную роль как раз в расчете ядерных реакций.
Известно, что ядра атомов всех элементов состоят из протонов и нейтронов. Число положительно заряженных протонов определяет общий электрический заряд ядра и вместе с тем место данного элемента в таблице Менделеева. Общее число протонов и нейтральных частиц— нейтронов определяет так называемое массовое число, близкое к атомному весу. Напомним, что массы атомов принято выражать в особых единицах, в которых масса ядра одного из изотопов кислорода равна точно 16 единицам. В тех же единицах выражают и массы протонов и нейтронов. Оказывается, что масса протона равна 1,00812, а масса нейтрона 1,00893 единицы (разумеется, речь идет о массах покоя).
Ядро атома того самого изотопа кислорода, чей атомный вес принят равным 16 единицам, состоит из 8 протонов и 8 нейтронов. Если мы сложим массы этих частиц, то получим 16,13640. Куда же девать остаток в 0,13640 единицы массы? Теория относительности объясняет этот дефект массы тем, что ядро атома содержит меньше энергии, чем «неорганизованный» набор частиц. Следовательно, при образовании ядра атома кислорода из соответствующего количества протонов и нейтронов обязательно должна выделяться энергия. И действительно» в процессе образования ядра появляется электромагнитное излучение. Для того чтобы разрушить, расщепить ядро на отдельные частицы, эту энергию нужно снова ему сообщить. Таким образом, дефект массы делает ядро устойчивым образованием, не позволяя ему самопроизвольно распадаться.
Рассмотрим одну из простейших термоядерных реакций. Ядро обычного водорода, состоящее из одного-единственного протона, соединяясь с ядром дейтерия — изотопа водорода, содержащим один протон и один нейтрон,— дает в результате ядро атома гелия, состоящее из двух протонов и одного нейтрона. Масса ядра водорода равна 1,00812, ядра дейтерия — 2,01471 и гелия— 3,01700. Легко подсчитать, что при этой реакции остается избыток массы в 0,00583 единицы. Следовательно, рассмотренная ядерная реакция сопровождается выделением энергии: при образовании 1 кг гелия выделяется количество энергии, эквивалентное 1,93 г.
Читатель легко переведет эту энергию в киловатт-часы.
Энергия при ядерных реакциях выделяется в виде излучения, а также переходит в кинетическую энергию образовавшихся ядер. Интересна в этом отношении реакция, при которой ядро водорода соединяется с ядром лития, имеющим массу в 7,01822 единицы. При этом образуется два ядра гелия с массами по 4,00390 единицы. Легко подсчитать, что эта реакция сопровождается выделением энергии в количестве 0,01854 массовой единицы. Оказывается, что здесь не возникает никакого излучения — вся энергия переходит в кинетическую энергию образовавшихся ядер, которые с огромной скоростью разлетаются в разные стороны. Скорость эту нетрудно вычислить. В самом деле, сумма релятивистских масс обоих атомов гелия должна быть равна сумме масс исходных ядер водорода и лития. Следовательно, релятивистская масса каждого ядра равна 4,00390 + 0,00927=4,01317. Отсюда имеем

Иногда, особенно в зарубежной литературе, подобные явления трактуются как переход массы в энергию. Говорят, что в данном случае избыток в 0,01854 единицы массы «перешел» в кинетическую энергию ядер гелия. Трудно представить себе более грубое извращение закона эквивалентности массы и энергии. Действительно, мы только что убедились, что закон сохранения массы ни в малейшей степени не нарушается, так что масса никуда не «переходит»; при этом, как всегда, имеется в виду релятивистская масса. В кинетическую энергию переходит не масса, а энергия исходных ядер. Дело, очевидно, заключается в том, что два ядра гелия содержат меньшее количество внутренней энергии, чем ядро водорода плюс ядро лития.
Мы хорошо знаем, что нужно различать массу покоя и релятивистскую массу. Точно так же следует различать внутреннюю и полную энергию тела или физической системы. Полная энергия складывается из внутренней энергии и кинетической энергии всей системы как целого. Полная энергия пропорциональна релятивистской массе, внутренняя — массе покоя, причем в обоих случаях коэффициентом пропорциональности является квадрат скорости света. Закону сохранения массы подчиняется лишь релятивистская масса; закону сохранения энергии — полная энергия. Внутренняя энергия не подчиняется закону сохранения по той простой причине, что она может переходить в энергию кинетическую.
В разобранном нами случае превращения водорода и лития в гелий часть внутренней энергии ядер водорода и лития переходит в кинетическую энергию ядер гелия. Одновременно часть массы покоя ядер водорода и лития идет на увеличение релятивистской массы ядер гелия сверх их массы покоя.
Таким образом, истинный смысл закона эквивалентности массы и энергии состоит отнюдь не в возможности «превращения» массы в энергию или обратно, а в том, что всякое превращение энергии из одного вида в другой непременно сопровождается соответствующим превращением масс. При этом масса и энергия всегда пропорциональны друг другу.
Другим явлением, которое также иногда истолковывается как превращение массы в энергию, является так называемая аннигиляция «элементарных» частиц. В настоящее время в физике твердо установлено, что для всякой частицы существует античастица. Так, наряду с электроном в свое время был открыт позитрон, имеющий одинаковую массу с электроном, но противоположный (положительный) заряд. Для протона античастицей служит антипротон — частица одинаковой с протоном массы, но опять-таки противоположно заряженная. Даже для нейтрона существует антинейтрон, отличающийся от него уже, конечно, не зарядом, а другими свойствами.
Когда какая-либо частица встречается со своей античастицей, то они взаимно притягиваются и, так сказать, «взаимно уничтожаются». Подлинного уничтожения, конечно, не происходит — вместо этих частиц возникают два или больше световых кванта. Здесь мы имеем дело с превращением вещества в другую форму материи — поле. Сумма энергий возникающих квантов в точности равна энергии аннигилирующих частиц; то же можно сказать и о их массе. Но световые кванты движутся со скоростью света, откуда сразу же следует, что их масса покоя равна нулю. Здесь, стало быть, внутренняя энергия частиц полностью переходит в чисто релятивистскую энергию света. Вместе с тем масса покоя частиц превращается также в чисто релятивистскую массу световых квантов. Опять-таки было бы ошибкой считать, что масса частиц перешла в энергию света. Как всегда, масса переходит в массу, а энергия — в энергию. Можно добавить, что наряду с аннигиляцией встречается и обратный процесс — рождения частиц из световых квантов; при этом частица появляется всегда в паре со своей античастицей. Все превращения массы и энергии происходят здесь в обратном порядке.
Закон эквивалентности массы и энергии справедливо считается одним из важнейших достижений теории относительности. Следует подчеркнуть, что он является в полном смысле новым законом. В то время как все соотношения теории относительности, с которыми мы имели дело прежде, переходят в соответствующие классические формулы, если скорость света считать бесконечно большой, для этого закона не существует никакого классического аналога.
Формула Эйнштейна Е=тс2 позволяет в любом релятивистском соотношении вместо массы подставить энергию и наоборот. Поэтому с чисто формальной точки зрения закон сохранения энергии тождествен с законом сохранения массы. Это не значит, однако, что масса вообще ничем не отличается от энергии. Масса есть мера инертности тела, а энергия — мера его способности совершать работу. Теория относительности устанавливает самую тесную связь между этими двумя свойствами, по она ни в коей мере не уничтожает разницы между ними. Дело здесь обстоит примерно так же, как и с различными видами энергии. Хорошо известно, например, что одна большая калория эквивалентна 4,2 ватт-секунды, но это не значит, что между тепловой и электрической энергией нет никакой качественной разницы, хотя мы и можем формально в любом физическом уравнении вместо энергии в калориях подставить энергию в ватт-секундах.
Как мы видели, закон эквивалентности массы и энергии играет основную роль при расчете энергии ядерных реакций; можно сказать даже, что этот закон впервые показал возможность использования ядерной энергии. Вместе с тем мы можем в настоящее время использовать лишь сравнительно небольшую долю внутренней энергии элементарных частиц. Перспектива выделения всей их внутренней энергии представляется, естественно, весьма заманчивой и в настоящее время составляет основной сюжетный стержень многих научно-фантастических романов, а также разного рода проектов, вроде «фотонной ракеты». Нужно, однако, помнить, что закон эквивалентности массы и энергии является далеко не единственным законом, с которым в этой области приходится считаться. Так, например, в ядерной физике основную роль играет закон сохранения заряда, согласно которому совершенно невозможно, например, превратить целое атомное ядро в электромагнитное излучение, так как последнее всегда электрически нейтрально, а ядро заряжено положительно. Кроме того, физике неизвестны процессы, при которых может в конечном итоге измениться общее число протонов и нейтронов.
В заключение вернемся еще раз к релятивистскому понятию силы. Мы видели, что масса и импульс составляют в теории относительности единый четырехмерный вектор. Вместо массы мы теперь можем подставить туда (с соответствующим коэффициентом) энергию и получить четырехмерный вектор энергии — импульса. Сила является, как известно, трехмерным вектором. Оказывается, что к этому вектору можно подобрать четвертую компоненту так, что получится уже вектор четырехмерный. Эта четвертая компонента представляет собой не что иное, как работу, произведенную в единицу времени, т. е. мощность. Мы приходим к четырехмерному вектору силы — мощности. Если 4-вектор энергии — импульса обозначить через р, а 4-вектор силы—мощности — через f, то второй закон Ньютона можно записать в следующем виде:
p2 - p1 = f(τ2 - τ1)
Это уравнение определяет одновременно как изменение импульса, так и изменение энергии. Так как собственное время х при изменении системы отсчета не меняется, то левая и правая части равенства при переходе к другой системе отсчета преобразуются совершенно одинаковым образом, согласно формулам Лоренца. Тем самым это уравнение автоматически оказывается справедливым во всех системах отсчета; оно, как говорят, ковариантно. Принцип относительности требует, чтобы все физические законы были одинаковы во всех системах отсчета. Математически это означает, что любое физическое уравнение можно было бы записать так, чтобы оно было справедливо в любой системе отсчета, т. е. в ковариантном виде. Это условие играет в теории относительности весьма существенную роль; с этим связало то значение, какое в теории относительности имеет векторное и тензорное исчисление.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|