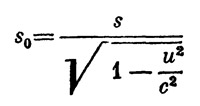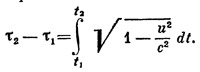Главная >> Введение в теорию относительности § 11. Собственное время
До сих пор понятие времени рассматривалось нами исключительно с «координатной» точки зрения. Наряду с тремя пространственными временная координата служит для фиксации событий; подобно пространственным координатам, время неразрывно связано с определенной системой отсчета и при перемене последней подвергается преобразованиям Лоренца.
Но в физических явлениях время играет не только координатную роль; этой стороной дела общее понятие времени еще не исчерпывается.
Пусть дано некоторое тело достаточно малых размеров; мы будем рассматривать его не как какую-то аморфную массу, а как сложную систему, в которой происходят различные физические процессы. Процессы эти могут проходить не иначе, как во времени. Следовательно, для нашего тела существует некоторое, соответствующее ему время.
Если тело движется равномерно и прямолинейно, мы можем «привязать» к нему систему отсчета; время этой системы и будет тогда, очевидно, тем временем, которое «действует» внутри нашего тела. Однако и при произвольном движении тела, вне зависимости от возможности связать с ним систему отсчета, соответствующее ему время, конечно, существует. Происходящие внутри тела процессы можно наблюдать и описывать с помощью различных систем отсчета; в различных системах темп этих процессов будет различен, так как они «подчиняются» времени не той или иной внешней системы отсчета, а своему собственному времени рассматриваемого тела.
Измерять собственное время можно, конечно, с помощью тех же самых приборов, какими вообще измеряется время. Разумеется, правильность и точность работы этих приборов зависит от физических условий, существующих внутри тела. Если, например, тело подвергается ускорениям, то это сильнейшим образом скажется на ходе маятниковых часов. Часы других конструкций могут быть менее чувствительны к ускорениям, но работу их могут нарушать, например, электромагнитные поля. Но этот вопрос относится уже к области методики и техники физических измерений и для нас не является сейчас принципиальным. Показания стрелки тех или иных часов еще не есть время, а лишь число, с той или иной степенью точности отражающее время. Мы же говорим о самом времени, которое определяется всей совокупностью физических процессов. Поэтому, говоря о показаниях часов, мы имеем в виду не какой-то конкретный часовой механизм, а «идеальные» часы, являющиеся, по существу, абстрактным понятием, единственным свойством которого является абсолютно точйое отображение времени.
Итак, с каждым материальным телом связано его собственное время. Собственное время не имеет отношения к системам отсчета, с помощью которых описывается движение тела; в частности, при изменении системы отсчета собственное время не должно меняться. В самом деле, если с нашим телом случились два события, между которыми стрелки установленных на нем часов (идеальных!) совершили десять оборотов, то этот факт не зависит от того, из какой системы отсчета мы за ним наблюдали. Собственное время есть величина абсолютная.
Время, связанное с той или иной системой отсчета, т. е. то самое время, о котором мы говорили в предыдущих параграфах, называется координатным временем. Оно является, как мы уже хорошо знаем, величиной относительной.
Как вычислять собственное время? Для этого нужно знать закон движения тела в некоторой (произвольно взятой) системе отсчета. Рассмотрим сначала случай, когда тело движется равномерно и прямолинейно. Тогда мы можем, кроме «основной» системы отсчета S, из которой мы все время наблюдаем за телом, ввести новую систему S*, в которой наше тело покоится. Координатное время системы S* будет совпадать с собственным временем нашего тела. Если с телом случились два События, координаты которых (в системе отсчета S) суть х1, t1 и x2, t2, то, обозначая через τ1 и τ2 соответствующие моменты собственного времени, имеем, очевидно
Переменим теперь «основную» систему отсчета. Тог да из формул преобразований Лоренца вытекает
Таким образом, интервал собственного времени выражается совершенно одинаково как через старые, так и через новые координаты. Это и значит, что он не зависит от системы отсчета.
В математике величины, не изменяющиеся при перемене системы координат, называются инвариантами. Таким образом, собственное время, в отличие от координатного, есть инвариант. Инвариантом является также упоминавшаяся в § 6 собственная длина. Если s — длина стержня, движущегося вдоль оси х со скоростью u, то величина
есть инвариант, т. е. не зависит от выбора системы отсчета, тогда как «обычная» длина s подвергается лоренцову сокращению. В дальнейшем мы познакомимся еще с некоторыми инвариантами.
В том случае, когда тело движется неравномерно, собственное время можно вычислять таким же способом, но полученную нами формулу надо применять к парам близких событий. Весь путь движения тела следует разбить на достаточно малые участки, на каждом из которых с достаточной точностью движение тела можно считать равномерным. Вычислив на каждом из этих участков собственное время по знакомой нам формуле, мы путем суммирования полученных элементарных интервалов можем получить общий интервал. Этот расчет будет тем точнее, чем меньше взятые участки. Точный результат мы получим, если найдем предел, к которому стремится вычисляемый интервал при все более мелком раздроблении. Нахождение таких пределов составляет основную задачу интегрального исчисления.
Для вычисления интервала собственного времени тела между моментами t1 и t2 координатного времени нужно, следовательно, вычислить интеграл
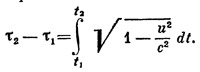 |
Полученное выше выражение для интервала собственного времени относится, собственно, лишь к бесконечно близким событиям; поэтому вместо разностей координат туда нужно подставить дифференциалы. Таким образом, в четырехмерном пространстве — времени квадрат интервала собственного времени имеет вид
dτ2=dt2 — 1/c2(dx2+dy2+dz2).
Понятие собственного времени во многом аналогично понятию длины дуги кривой. Обратимся к следующему примеру. Каждая точка земной поверхности определяется двумя координатами — широтой и долготой. Выбор градусной сетки связан в первую очередь с вращением Земли — на полюсах сходятся все меридианы, а от экватора, расположенного посредине, отсчитываются широты. Начало отсчета долгот выбрано более или менее произвольно. Никто не мешает выбрать и другую координатную сетку. Представим себе на минуту, что осуществилась мечта героев романа Жюля Верна «Вверх дном» и что ось вращения Земли изменилась. Тогда придется, по-видимому, менять и градусную сетку соответственно новым положениям полюсов. Все пункты земной поверхности получат новые координаты.
Но ведь географические координаты имеют чисто вспомогательное значение. Когда мореплаватель с помощью секстана и хронометра определяет широту и долготу своего судна, те цифры, которыми они выражаются, сами по себе его не интересуют. Они нужны ему лишь для того, чтобы нанести положение судна на карту и определить тем самым окружающую обстановку, расстояние до нужного пункта и т. д. Все это с одинаковым успехом можно проделать в любой системе координат. Разность широт Ленинграда и Москвы составляет примерно 4°, при другой координатной сетке она будет другой, но тот факт, что от Москвы до Ленинграда 660 километров, не имеет никакого отношения ни к широте, ни к долготе. Правда, зная точные географические координаты Москвы и Ленинграда, мы всегда можем, пользуясь соответствующими формулами, это расстояние вычислить. Результат не будет, конечно, зависеть от того, какой градусной сеткой мы при этом будем пользоваться. Таким же образом можно вычислять и более сложные величины: длины рек, железнодорожных путей, площади озер и морей и т. д.
Наши системы отсчета представляют собой не что иное, как инструмент для определения координат событий. Оли служат для «наложения» координатной сетки на весь наш четырехмерный мир. У каждой системы отсчета такая сетка своя, и координаты событий в разных системах отсчета различны. Но собственное время определяется мировой линией данного тела и не зависит от выбора сетки. В некотором смысле можно рассматривать собственное время как нечто вроде длины отрезка мировой линии. Оговоримся сразу же, что эта «длина» обладает многими не совсем обычными свойствами. В то же время аналогия между длиной и собственным временем не так уже поверхностна; согласно современным геометрическим представлениям, между этими двумя понятиями нет принципиальной разницы.
Представим себе два тела, начинающие двигаться из одной и той же точки пространства и через некоторое время вновь встречающиеся в другой точке. Мировые линии этих тел будут пересекаться в двух точках. Отрезки их между точками пересечения не обязаны иметь одинаковые «длины». Значит, интервалы собственного времени, отсчитанные по часам каждого из двух тел, будут, вообще говоря, различны.
Из геометрии известно, что из всех линий, соединяющих две данные точки, прямая имеет наименьшую длину. Оказывается, и собственное время обладает аналогичным свойством. Выберем две мировые точки и будем соединять их различными временноподобными мировыми линиями. Можно совершенно строго доказать, что собственное время, отсчитанное вдоль прямой мировой линии, будет наибольшим. Если мы снова вернемся к нашим дважды встречающимся телам и предположим, что одно из них между встречами движется равномерно и прямолинейно, то окажется, что установленные на нем часы покажут наибольшее собственное время между встречами, чем часы всякого другого тела.
Таким образом, аналогия между собственным временем и длиной несколько своеобразна — получается, что прямая линия имеет как бы наибольшую длину. Это обстоятельство не снижает, тем не менее, ценности этой аналогии. Дело просто в том, что геометрия пространства — времени не является евклидовой, хотя геометрия одного «чистого» пространства евклидова.
Мало того. Рассмотрим мировую линию светового сигнала. Для любых ее двух точек имеет место соотношение х2—x1 = c (t2—t1). После подстановки в выражение интервала собственного времени мы легко убедимся, что интервал этот всегда равен нулю. Существуют, стало быть, мировые линии, обладающие нулевой длиной. Если позволить себе выражаться несколько образно и не совсем строго, то можно сказать, что свет при своем движении не затрачивает совершенно своего времени. От далеких звезд и галактик до нас, земных наблюдателей, свет идет десятки, сотни и тысячи лет.
Но это лишь с нашей точки зрения. Если бы какой-нибудь ловкий «наблюдатель» сумел оседлать световой луч, то эти невообразимые расстояния он преодолел бы мгновенно. Перспектива эта весьма привлекательна, в особенности для писателей-фантастов. К сожалению, их придется разочаровать — вместе с таким результатом теория относительности делает к нему примечание о том, что ни одно материальное тело не может достичь скорости света. Не следует этим особенно огорчаться — теория относительности не запрещает приближаться к скорости света как угодно близко, а возможность попутешествовать в пространстве по достаточно кривой мировой линии лет десять и вернуться на Землю, которая к тому времени успеет постареть лет на сто, тоже достаточно соблазнительна.
Теперь вспомним первый закон Ньютона — закон инерции. Он утверждает, что всякое тело стремится двигаться равномерно и прямолинейно. Но вдоль прямой мировой линии интервал собственного времени принимает максимальное значение. Следовательно, мы можем дать закону инерции и другую формулировку. Можно сказать, что всякое тело стремится двигаться так, чтобы его собственное время текло всего быстрее. Образно говоря, всякое тело стремится как можно быстрее постареть.
Вероятно, не всем читателям понравится такой физический закон. Чем же можно их утешить? Можно посоветовать: не двигайтесь по инерции, старайтесь двигаться ускоренно! Придерживаясь этого мудрого правила, вы наверняка за свою жизнь сэкономите несколько микросекунд...
С первого взгляда новая формулировка закона инерции кажется просто смешной и курьезной. В свое время мы, однако, убедимся, что это не так. Главная ее ценность состоит в том, что она не нуждается ни в какой системе отсчета. Кроме того, она имеет самое непосредственное отношение к одному весьма важному и общему закону физики — так называемому закону наименьшего действия.
В § 7, обсуждая вопрос о релятивистском замедлении времени, мы коснулись так называемого «парадокса часов». Теперь этот вопрос предстает перед нами в новом свете. Мы сравнивали показания двух часов, одни из которых были неподвижны, а другие, отправляясь из той же точки, после некоторого путешествия возвращались обратно. Теперь ясно, что большее время покажут неподвижные часы, т. е. движущиеся часы отстанут. Этот факт не зависит совершенно от выбора системы отсчета — важно лишь, что первые часы движутся по ийерции.
Итак, в теории относительности существуют два времени: относительное координатное время и абсолютное собственное время. Физический смысл и роль этих двух понятий совершенно различны. Связь между ними устанавливается тем, что собственное время покоящегося в некоторой системе отсчета тела совпадает с координатным временем этой системы отсчета. Отметим в заключение, что отношение одновременности принадлежит исключительно координатному времени, поскольку оно относится обязательно к двум различным телам. Поэтому одновременность двух событий зависит от системы отсчета.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|