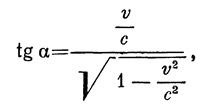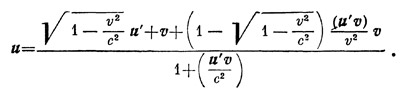Главная >> Введение в теорию относительности § 10. Закон сложения скоростей
Преобразования Лоренца дают нам возможность вычислять изменение координат события при переходе от одной системы отсчета к другой. Поставим теперь вопрос о том, как при изменении системы отсчета будет меняться скорость одного и того же тела?
В классической механике, как известно, скорость тела просто складывается со скоростью системы отсчета. Сейчас мы убедимся, что в теории относительности скорость преобразуется по более сложному закону.
Мы снова ограничимся рассмотрением одномерного случая. Пусть две системы отсчета S и S` «наблюдают» за движением некоторого тела, которое перемещается равномерно и прямолинейно параллельно осям х и х` обеих систем отсчета. Пусть скорость тела, измеренная системой отсчета S, есть и; скорость того же тела, измеренную системой S`, обозначим через и` . Буквой v будем по-прежнему обозначать скорость системы S` относительно S.
Допустим, что с нашим телом происходят два события, координаты которых в системе S суть x1,t1, и х2, t2. Координаты тех же событий в системе S` пусть будут х`1, t`1; x`2, t`2. Но скорость тела есть отнощение пройденного телом пути к соответствующему промежутку времени; поэтому, чтобы найти скорость тела в той и другой системах отсчета, нужно разность пространственных координат обоих событий разделить на разность временных координат

которую можно, как всегда, получить из релятивистской, если скорость света считать бесконечной. Ту же формулу можно записать в виде
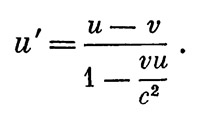 |
Для небольших, «обычных» скоростей обе формулы— релятивистская и классическая — дают практически совпадающие результаты, в чем читатель при желании легко сможет убедиться. Но при скоростях, близких к скорости света, разница становится весьма ощутимой. Так, если v=150 000 км/сек, u`=200 000 км/сек, то вместо классического результата u = 350 000 км/сек релятивистская формула дает u = 262 500 км/сек. Согласно смыслу формулы сложения скоростей, этот результат означает следующее.
Пусть система отсчета S` движется относительно системы отсчета S со скоростью v = 150 000 км/сек. Пусть в том же направлении движется тело, причем измерение его скорости системой отсчета S` дает результат u =200 000 км/сек. Если теперь измерить скорость того же тела с помощью системы отсчета S то получится u=262 500 км/сек.
Следует подчеркнуть, что полученная нами формула предназначена именно для пересчета величины скорости одного и того же тела от одной системы отсчета к другой, а отнюдь не для вычисления «скорости сближения» или «удаления» двух тел. Если мы из одной и той же системы отсчета наблюдаем два движущихся навстречу друг другу тела, причем скорость одного тела равна 150 000 км/сек, а второго — 200 000 км/сек, то расстояние между этими телами каждую секунду будет уменьшаться на 350 000 км. Теория относительности не упраздняет законов арифметики.
Читатель уже понял, конечно, что, применяя эту формулу к скоростям, не превосходящим скорость света, мы снова получим скорость, не превосходящую с. Не представляет никакого труда доказать это утверждение вполне строго. Действительно, легко проверить.
Для небольших, «обычных» скоростей обе формулы— релятивистская и классическая — дают практически совпадающие результаты, в чем читатель при желании легко сможет убедиться. Но при скоростях, близких к скорости света, разница становится весьма ощутимой. Так, если v=150 000 км/сек, u`=200 000 км/сек, то вместо классического результата u = 350 000 км/сек релятивистская формула дает u = 262 500 км/сек. Согласно смыслу формулы сложения скоростей, этот результат означает следующее.
Пусть система отсчета S` движется относительно системы отсчета S со скоростью v = 150 000 км/сек. Пусть в том же направлении движется тело, причем измерение его скорости системой отсчета S` дает результат u` =200 000 км/сек. Если теперь измерить скорость того же тела с помощью системы отсчета S то получится u=262 500 км/сек.
Следует подчеркнуть, что полученная нами формула предназначена именно для пересчета величины скорости одного и того же тела от одной системы отсчета к другой, а отнюдь не для вычисления «скорости сближения» или «удаления» двух тел. Если мы из одной и той же системы отсчета наблюдаем два движущихся навстречу друг другу тела, причем скорость одного тела равна 150 000 км/сек, а второго — 200 000 км/сек, то расстояние между этими телами каждую секунду будет уменьшаться на 350 000 км. Теория относительности не упраздняет законов арифметики.
Читатель уже понял, конечно, что, применяя эту формулу к скоростям, не превосходящим скорость света, мы снова получим скорость, не превосходящую с. Не представляет никакого труда доказать это утверждение вполне строго. Действительно, легко проверить, что имеет место равенство
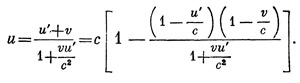 |
Так как и` ≤ с и v < c, то в правой части равенства числитель и знаменатель, а с ними и вся дробь, неотрицательны. Поэтому квадратная скобка меньше единицы, а потому и ≤ с .
Если и`=с, то и и=с. Это есть не что иное, как закон постоянства скорости света. Не следует, конечно, рассматривать этот вывод как «доказательство» или хотя бы «подтверждение» постулата постоянства скорости света. Ведь мы с самого начала исходили из этого постулата и неудивительно, что пришли к результату, который ему не противоречит, в противном случае этот постулат был бы опровергнут путем доказательства от противного. Вместе с тем мы видим, что закон сложения скоростей эквивалентен постулату постоянства скорости света, каждое из этих двух утверждений логически вытекает из другого (и остальных постулатов теории относительности).
При выводе закона сложения скоростей мы предполагали, что скорость тела параллельна относительной скорости систем отсчета. Этого предположения можно было ие делать, но тогда наша формула относилась бы лишь к той компоненте скорости, которая направлена по оси x, и формулу следовало бы записать в виде
С помощью этих формул мы разберем явление аберрации (см. § 3). Ограничимся лишь простейшим случаем. Пусть некоторое светило в системе отсчета S неподвижно, пусть, далее, система отсчета S` движется относительно системы S со скоростью v и пусть наблюдатель, движущийся вместе с S`, принимает лучи света от светила как раз в тот момент, когда оно находится у него точно над головой (рис. 21). Составляющие скорости этого луча в системе S будут
ux = 0, uy = 0, ux = -c.
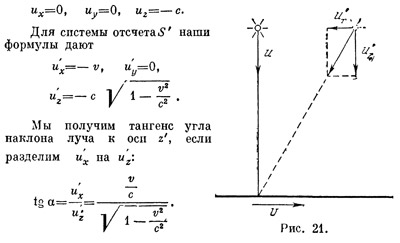 |
Для системы отсчета S` наши формулы дают
u`x = -v, u`y = 0,
u`z = -c√(1 - v2/c2)
Мы получим тангенс угла наклона луча к оси z`, если разделим и`х на и`z:
tg α = и`х / и`z = (v/c) / √(1 - v2/c2)
Если скорость v не очень велика, то можно применить известную нам приближенную формулу, с помощью которой получаем
tg α = v/c + 1/2*v2/c2.
Первое слагаемое представляет собой хорошо известный классический результат; второе слагаемое есть релятивистская поправка.
Орбитальная скорость Земли равна примерно 30 км/сек, так что (v/c) = 10-4. Для малых углов тангенс равен самому углу, измеренному в радианах; так как радиан содержит круглым счетом 200 000 угловых секунд, то получаем для угла аберрации:
α = 20°
Релятивистская поправка в 20 000 000 раз меньше и лежит далеко за пределами точности астрономических измерений. Вследствие аберрации звезды описывают ежегодно на небе эллипсы с большой полуосью в 20".
Когда мы смотрим на движущееся тело, мы видим его не там, где оно находится в данный момент, а там, где оно было несколько раньше, ибо свету нужно некоторое время, чтобы Дойти от тела до наших глаз. Это явление с точки зрения теории относительности эквивалентно аберрации и сводится к ней при переходе к той системе отсчета, в которой рассматриваемое тело неподвижно. На основании этого простого соображения мы можем получить формулу аберрации совершенно элементарным путем, не прибегая к релятивистскому закону сложения скоростей.
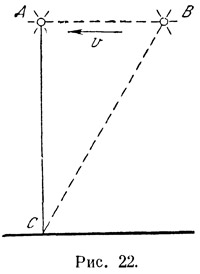 Пусть наше светило движется параллельно земной поверхности справа налево (рис. 22). Когда оно прибывает в точку А, наблюдатель, находящийся точно под ним в точке С, видит его еще в точке В. Если скорость светила равна v, а промежуток времени, в течение которого оно проходит отрезок АВ, равен Δt, то Пусть наше светило движется параллельно земной поверхности справа налево (рис. 22). Когда оно прибывает в точку А, наблюдатель, находящийся точно под ним в точке С, видит его еще в точке В. Если скорость светила равна v, а промежуток времени, в течение которого оно проходит отрезок АВ, равен Δt, то
AB = Δt,
BC=cΔt,
sin α = AB/BC = v/c.
Но тогда, согласно формуле тригонометрии,
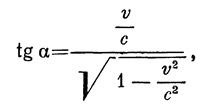 |
что и требовалось доказать. Заметим, что в классической кинематике эти две точки зрения не эквивалентны.
Интересен также следующий вопрос. Как известно, в классической кинематике скорости складываются по правилу параллелограмма. Мы заменили этот закон другим, более сложным. Значит ли это, что в теории относительности скорость уже не есть вектор?
Во-первых, то обстоятельство, что u ≠ u`+v (жирными буквами мы обозначаем векторы), само по себе не дает еще оснований отрицать векторную природу скорости. Из двух данных векторов третий вектор можно получить не только путем их сложения, а, например, путем векторного умножения, и вообще бесчисленным множеством способов. Ниоткуда не следует, что при перемене системы отсчета векторы и` и v обязаны именно складываться. И действительно, существует формула, выражающая и через и` и v с помощью операций векторного исчисления:
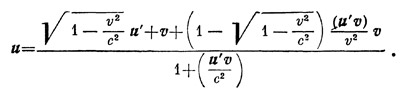 |
В связи с этим следует признать, что название «закон сложения скоростей» не совсем удачно; правильнее говорить, как это и делают некоторые авторы, не о сложении, а о преобразовании скорости при перемене системы отсчета.
Во-вторых, и в теории относительности можно указать случаи, когда скорости складываются по-прежнему векторно. Пусть, например, тело двигалось в течение некоторого промежутка времени Δt со скоростью u1, а затем — такой же отрезок времени со скоростью u2. Это сложное движение можно заменить движением с постоянной скоростью u = u1+ u2. Здесь скорости u1 и u2 складываются, как векторы, по правилу параллелограмма; теория относительности не вносит здесь никаких изменений.
Следует вообще заметить, что большинство «парадоксов» теории относительности связано так или иначе с изменением системы отсчета. Если рассматривать явления в одной и той же системе отсчета, то вносимые теорией относительности изменения в их закономерности далеко не столь кардинальны, как часто думают.
Отметим еще, что естественным обобщением обычных трехмерных векторов в теории относительности являются векторы четырехмерные; при перемене системы отсчета они преобразуются по формулам Лоренца. Кроме трех пространственных компонент, они имеют компоненту временную. В частности, можно рассматривать четырехмерный вектор скорости. Пространственная «часть» этого вектора, однако, не совпадает с обычной трехмерной скоростью, и вообще четырехмерная скорость по своим свойствам заметно отличается от трехмерной. В частности, сумма двух четырехмерных скоростей не будет уже, вообще говоря, скоростью.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





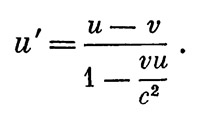
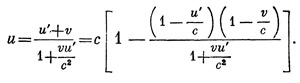
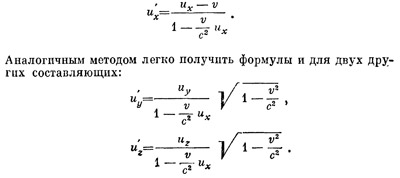

 Пусть наше светило движется параллельно земной поверхности справа налево (рис. 22). Когда оно прибывает в точку А, наблюдатель, находящийся точно под ним в точке С, видит его еще в точке В. Если скорость светила равна v, а промежуток времени, в течение которого оно проходит отрезок АВ, равен Δt, то
Пусть наше светило движется параллельно земной поверхности справа налево (рис. 22). Когда оно прибывает в точку А, наблюдатель, находящийся точно под ним в точке С, видит его еще в точке В. Если скорость светила равна v, а промежуток времени, в течение которого оно проходит отрезок АВ, равен Δt, то