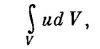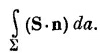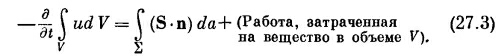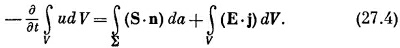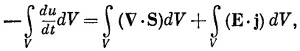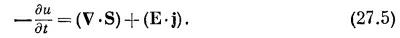Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 27. Энергия поля и его импульс

Сохранение энергии и электромагнитное поле

Нам надо теперь описать сохранение энергии в электромагнитном поле количественно. Для этого нужно выяснить, сколько энергии находится в единице объема, а также какова скорость ее потока. Рассмотрим сначала энергию только электромагнитного поля. Пусть и обозначает плотность энергии поля, т. е. количество энергии в единице объема пространства, а вектор S — поток энергии поля (т. е. количество энергии, прошедшее в единицу времени через единичную поверхность, перпендикулярную к потоку). Тогда, аналогично сохранению заряда (27.1), можно написать «локальный» закон сохранения энергии поля в виде

Конечно, этот закон, вообще говоря, не верен; энергия поля не сохраняется. Представьте, что вы находитесь в темной комнате, а затем поворачиваете выключатель. Комната внезапно наполняется светом, т. е. в ней оказывается энергия поля, которой раньше не было. Уравнение (27.2) не составляет полного закона сохранения, ибо энергия одного только поля не сохраняется, а существует еще энергия вещества; сохраняется лишь полная энергия во всем мире. Энергия поля будет изменяться, если оно производит работу над веществом или вещество производит работу над полем.
 
Однако если внутри интересующего нас объема находится вещество, то мы знаем, сколько энергии оно несет в себе: энергия каждой частицы равна m₀c²/√1—v²/c². Полная же энергия вещества равна просто сумме энергий всех частиц, а поток ее через поверхность равен просто сумме энергий, переносимой каждой частицей, пересекающей эту поверхность. Но сейчас мы будем иметь дело только с энергией электромагнитного поля. Так что мы должны написать уравнение, которое говорит, что полная энергия поля в данном объеме уменьшается либо в результате вытекания ее из объема, либо потому, что поле передает свою энергию веществу (или приобретает ее, что означает просто отрицательную потерю). Энергия поля в объеме V равна

а скорость ее уменьшения равна производной этого интеграла по времени со знаком минус. Поток энергии поля из объема V равен интегралу от нормальной компоненты S по поверхности ∑,  ограничивающей объем V:

Таким образом,

Раньше мы видели, что над каждой единицей объема вещества поле в единицу времени производит работу Е ·j. [Сила, действующая на частицу, равна F=q(E+vXB), а мощность равна F·v=qE·v. Если в единице объема содержится N частиц, то эта мощность в единице объема равна NqE ·v, a Nqv=j.] Таким образом, величина Е·j должна быть равна энергии, теряемой полем в единице объема за единицу времени. Уравнение (27.3) при этом приобретает вид

Вот как выглядит наш закон сохранения энергии в поле. Его можно записать как дифференциальное уравнение, подобное (27.2); для этого второе слагаемое нужно превратить в интеграл по объему, что легко делается с помощью теоремы Гаусса. Поверхностный интеграл от нормальной компоненты S равен интегралу от дивергенции S по объему, ограниченному этой поверхностью, так что уравнение (27.3) эквивалентно следующему:

где производную по времени от первого слагаемого мы внесли под интеграл. Поскольку это уравнение верно для любого объема, то интегралы можно отбросить и получить уравнение для энергии электромагнитного поля:

Однако это уравнение не даст нам ничего хорошего, пока мы не узнаем, что такое и и S. Быть может, мне следовало бы просто сказать вам, как они выражаются через Е и В, поскольку это единственное, что нам, собственно, нужно. Однако мне очень хочется изложить вам все те рассуждения, которыми в 1884 г. воспользовался Пойнтинг, чтобы получить формулы для S и u, с тем чтобы вы понимали, откуда они взялись. (Для дальнейшей работы, впрочем, вам этот вывод не потребуется.)

СМОТРИТЕ ТАКЖЕ: