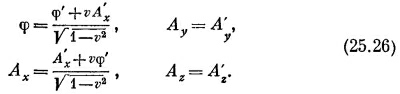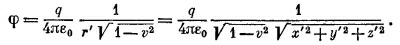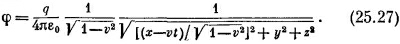| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Четырехмерный потенциал движущегося заряда
Теперь выпишем законы преобразования, выражающие φ и А в движущейся системе через φ и А в неподвижной, хотя неявно мы уже говорили о них. Поскольку Аμ=(φ, А) является четырехвектором, это уравнение должно выглядеть подобно (25.1), за исключением того, что t нужно заменить на φ, а х — на А. Таким образом,
причем r` — расстояние от заряда q до точки в движущейся системе, где производится измерение поля. Векторный же потенциал А′, разумеется, равен нулю.
Используя далее выражение для φ′[см. (25.25)] и равенство А′=0, получаем
Эта формула дает нам скалярный потенциал φ, который мы увидели бы в системе S, но он, к сожалению, записан через координаты штрихованной системы. Впрочем, это дело легко поправимо; с помощью (25.1) можно выразить t′, x′, у′, z′ через t, x, у, z и получить
Повторяя ту же процедуру для вектора А, вы можете показать,
Это те же самые формулы, которые мы вывели в гл. 21, но там они были получены другим методом. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

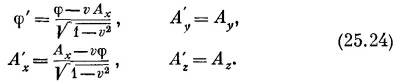
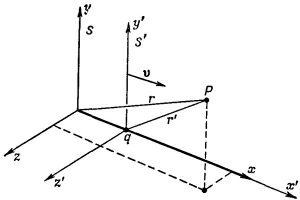 При этом предполагается, что штрихованная система координат движется по отношению к нештрихованной со скоростью v в направлении оси х.
При этом предполагается, что штрихованная система координат движется по отношению к нештрихованной со скоростью v в направлении оси х.