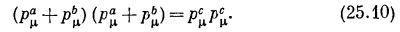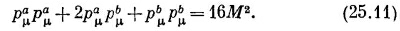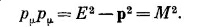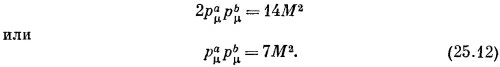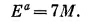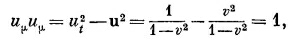| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Скалярное произведение
То, что расстояние от некоторой точки до начала координат не изменяется при повороте, если хотите,— счастливая случайность. Математически это означает, что r2=x2+y2+z2 является инвариантом. Другими словами, после поворота r′2=r2 или
Возникает вопрос: существует ли подобная величина, которая инвариантна при преобразованиях Лоренца? Да, существует. Из (25.1) вы видите, что
Она была бы всем хороша, если бы только не зависела от нашего выбора оси х. Но этот недостаток легко исправить вычитанием у2 и z2. Тогда преобразование Лоренца плюс вращение оставляют ее неизменной. Таким образом, роль величины, аналогичной трехмерному r2 в четырехмерном пространстве, играет комбинация
Она является инвариантом так называемой «полной группы Лоренца», которая включает как перемещения с постоянной скоростью, так и повороты.
Эту величину мы будем называть квадратом «длины» четырехвектора аμ . (Будьте внимательны! Иногда берут обратные знаки у всех слагаемых и квадратом длины называют число ax2+ay2 +az2 –at2.)
также будет инвариантной (скалярной) величиной. (Фактически мы доказали это уже в гл. 17, вып. 2.) Получилась величина, совершенно аналогичная скалярному произведению векторов. Мы так и будем называть ее скалярным произведением двух четырехвекторов. Логично, казалось бы, и записывать его аμ ·bμ , чтобы оно даже выглядело похожим на скалярное произведение. Но обычно, к сожалению, так не делают и пишут его без точки. И мы тоже будем придерживаться этого порядка и записывать скалярное произведение просто аμbμ . Итак, по определению,
Помните, что повсюду, где вы видите два одинаковых значка (вместо μ, мы иногда будем пользоваться v или другими буквами), необходимо взять четыре произведения и сложить их, не забывая при этом о знаке минус перед произведениями пространственных компонент. С учетом такого соглашения инвариантность скалярного произведения при преобразованиях Лоренца можно записать как
Поскольку последние три слагаемых в формуле (25.7) представляют просто трехмерное скалярное произведение, то часто удобнее принять такую запись:
Очевидно, что введенную выше четырехмерную длину можно записать как аμаμ:
Но иногда удобно эту величину записать как аμ2:
Продемонстрируем теперь плодотворность четырехмерного скалярного произведения. Антипротоны (р) получают на больших ускорителях из реакции
Иначе говоря, высокоэнергетический протон сталкивается с покоящимся протоном (например, с помещенной в пучок водородной мишенью), и если падающий протон обладает достаточной энергией, то вдобавок к двум первоначальным протонам может родиться пара протон—антипротон.
а комбинируя эти два выражения, можно написать
Теперь еще одно важное обстоятельство: поскольку мы получили уравнение для четырехвекторов, то оно должно выполняться в любой инерциальной системе. Этим фактом можно воспользоваться для упрощения вычислений. Напишем длины каждой из частей (25.9), которые, разумеется, тоже должны быть равны друг другу, т. е.
Так как рμc рμc— инвариант, то можно вычислить его в какой-то одной системе координат. В системе ц. м. временная компонента рμc равна энергии покоя четырех протонов, т. е. 4М, а пространственная часть р равна нулю, так что рμ¦c=(4М, 0). При этом мы воспользовались равенством масс протона и антипротона, обозначив их одной буквой М.
Произведения рμa рμa и рμb рμb, вычисляются очень быстро: «длина» четырехвектора импульса любой частицы равна просто квадрату ее массы:
Это можно доказать прямыми вычислениями или, несколько более эффектно, простым замечанием, что в системе покоя частицы рμ =(М, 0), а следовательно, рμрμ=М2. А так как это инвариант, то он равен М2 в любой системе отсчета. Подставляя результаты в уравнение (25.11), мы получаем
Теперь можно вычислить рμaрμb в лабораторной системе. В этой системе четырехвектор рμa = (Еа, рa), а рμb,=(М, 0), ибо он описывает покоящийся протон. Итак, рμaрμb должно быть равно МЕа, а мы знаем, что скалярное произведение — это инвариант, поэтому оно должно быть равно значению, найденному нами в (25.12). В результате получается
Полная энергия падающего протона должна быть по меньшей мере равна 7М (что составляет около 6,6 Гэв, так как М=938 Мэв) или после вычитания массы покоя М получаем, что кинетическая энергия должна быть равна по меньшей мере 6М (около 5,6 Гэв). Именно с тем, чтобы иметь возможность производить антипротоны, беватрон в Беркли проектировался на кинетическую энергию ускоренных протонов около 6,2 Гэв.
т. е. иμ — единичный четырехвектор. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

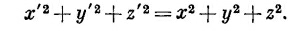
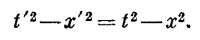
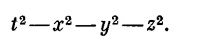
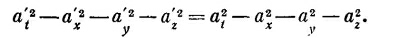
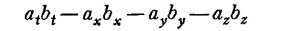
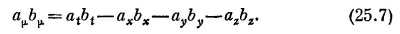
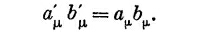
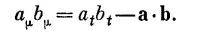
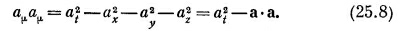
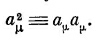
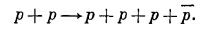
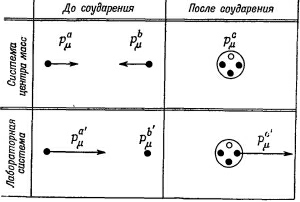 Ответ легче всего получить, рассмотрев эту реакцию в системе центра масс (ц. м.) (фиг. 25.1). Назовем падающий протон протоном а, а его четырехимпульс обозначим через рμa. Аналогично, протон мишени назовем b, а его четырехимпульс обозначим через рμb,. Если энергии падающего протона как раз достаточно для реакции, то в конечном состоянии (т. е. в состоянии после соударения) образуется система, содержащая три протона и антипротон, покоящиеся в системе ц. м. Если энергия падающего протона будет несколько выше, то частицы в конечном состоянии вылетят с некоторой кинетической энергией и будут разлетаться в стороны; если же она немного ниже, то ее будет недостаточно для образования четырех частиц.
Ответ легче всего получить, рассмотрев эту реакцию в системе центра масс (ц. м.) (фиг. 25.1). Назовем падающий протон протоном а, а его четырехимпульс обозначим через рμa. Аналогично, протон мишени назовем b, а его четырехимпульс обозначим через рμb,. Если энергии падающего протона как раз достаточно для реакции, то в конечном состоянии (т. е. в состоянии после соударения) образуется система, содержащая три протона и антипротон, покоящиеся в системе ц. м. Если энергия падающего протона будет несколько выше, то частицы в конечном состоянии вылетят с некоторой кинетической энергией и будут разлетаться в стороны; если же она немного ниже, то ее будет недостаточно для образования четырех частиц.