Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 22. Цепи переменного тока Генераторы
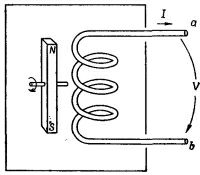 Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе. Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе.
Пусть у нас имеется катушка, наподобие катушки самоиндукции но только витков у нее немного и на магнитное поле ее собственного тока можно внимания не обращать. Эта катушка, однако, находится в переменном магнитном поле подобном тому какое создается вращающимся магнитом (фиг. 22.5). (Мы уже видели ранее, что такое вращающееся магнитное поле можно также создать с помощью подходящей совокупности катушек с переменными токами.) Сделаем снова несколько упрощающих допущений. Это все те же допущения, которые мы делали, говоря об индуктивности. В частности, мы предполагаем, что меняющееся магнитное поле ограничено лишь небольшой областью поблизости от катушки и за пределами генератора, в пространстве между клеммами, оно не чувствуется.
Повторяя опять в точности тот же анализ, что и для индуктивности, рассмотрим контурный интеграл от Е вдоль замкнутой петли, которая начинается на зажиме а, проходит по катушке до зажима b и возвращается к началу по пространству между зажимами. Снова заключаем, что разность потенциалов между зажимами а и b равна всему интегралу от Е вдоль петли:
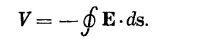 |
Этот контурный интеграл равен э.д.с. в цепи, и поэтому разность потенциалов V между выводами генератора тоже равна скорости изменения магнитного потока сквозь катушку:
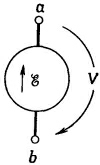 Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. Ε(t). Такой идеальный генератор представляют символом, показанным на фиг. 22.6. Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V=Ε с более высоким потенциалом на зажиме а. Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. Ε(t). Такой идеальный генератор представляют символом, показанным на фиг. 22.6. Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V=Ε с более высоким потенциалом на зажиме а.
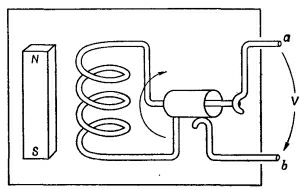 Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7). Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7).
Мы изобразили магнитную палочку, чтобы показать наличие магнитного поля, но его можно, конечно, заменить любым другим источником постоянного магнитного поля, скажем добавочной катушкой, по которой течет постоянный ток. Как показано на рисунке, вращающаяся катушка связана с внешним миром скользящими контактами, или «кольцами». Нас опять интересует разность потенциалов, которая появляется между клеммами а и b, т. е. интеграл от электрического поля между а и b по пути снаружи генератора.
Теперь в этой системе уже нет изменяющихся магнитных полей и на первый взгляд кажется удивительным, откуда на зажимах генератора берется напряжение. Действительно, ведь нигде же внутри генератора нет никаких электрических полей. Мы, как обычно, предполагаем для наших идеальных элементов, что внутри них провода сделаны из идеально проводящего материала; а, как уже неоднократно повторялось, электрическое поле внутри идеального проводника равно нулю. Но это не всегда верно. Это неверно тогда, когда проводник движется в магнитном поле. Правильное утверждение таково: общая сила, действующая на произвольный заряд внутри идеального проводника, должна быть равна нулю. Иначе в нем возник бы бесконечный ток свободных зарядов. Так что надо брать сумму электрического поля Е и векторного произведения скорости проводника v на магнитное поле В; это есть полная сила, действующая на единичный заряд, и вот она-то всегда равна нулю:
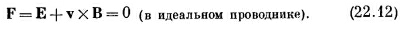 |
А наше прежнее утверждение о том, что внутри идеальных проводников электрических полей не бывает, верно лишь тогда, когда скорость проводника v равна нулю; в противном случае справедливо выражение (22.12).
Вернемся к нашему генератору, показанному на фиг. 22.7. Теперь мы видим, что контурный интеграл от электрического поля Е между зажимами а и b по проводящим путям генератора должен быть равен контурному интегралу от vXB по тому же пути:
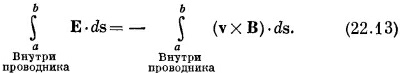 |
Однако по-прежнему остается верным, что контурный интеграл от Е по замкнутой петле, включая возвращение от зажима b к а вне генератора, должен быть равен нулю, потому что меняющиеся магнитные поля отсутствуют. Так что первый интеграл в (22.13) по-прежнему равен V — напряжению на зажимах. Оказывается, что интеграл в правой части (22.13) просто равен быстроте изменения потока через катушку, а значит, по правилу потока, равен э.д.с. катушки. И опять получается, что разность потенциалов между зажимами равна э.д.с. цепи в согласии с уравнением (22.11). Так что все равно, какой у нас генератор: меняется ли в нем магнитное поле возле закрепленной катушки, вертится ли в закрепленном магнитном поле катушка,— внешние свойства генераторов одни и те же. На клеммах всегда существует напряжение V, которое не зависит от тока в цепи, а определяется только условиями внутри генератора, формируемыми по нашему произволу.
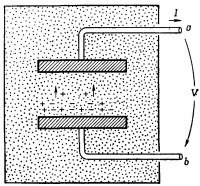 Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8. Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента. Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8. Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента.
Рассуждая так же, как это мы делали, когда говорили об идеальном конденсаторе, мы убедимся, что, если нет избытка диффузии ионов какого-либо знака, разность потенциалов между зажимами а и b равна просто контурному интегралу от электрического поля между электродами. Конечно, между конденсатором и таким химическим элементом есть существенная разница. Если на мгновение закоротить выводы конденсатора, он разрядится и разности потенциалов между выводами уже не будет. В случае же химического элемента ток с зажимов можно снимать непрерывно, никак не изменяя при этом э.д.с, пока, конечно, реактивы в элементе не израсходуются. Известно, что в реальном элементе разность потенциалов на зажимах убывает по мере возрастания снимаемого с него тока. Но при нашей идеализации задачи легко себе представить, что у нас есть идеальный элемент, в котором напряжение на электродах не зависит от силы тока. Тогда реальный элемент можно рассматривать как идеальный, соединенный последовательно с сопротивлением.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе.
Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе.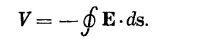
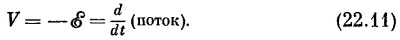
 Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. Ε(t). Такой идеальный генератор представляют символом, показанным на фиг. 22.6. Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V=Ε с более высоким потенциалом на зажиме а.
Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. Ε(t). Такой идеальный генератор представляют символом, показанным на фиг. 22.6. Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V=Ε с более высоким потенциалом на зажиме а. Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7).
Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7).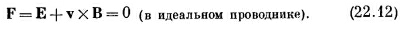
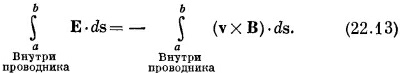
 Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8. Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента.
Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8. Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента.