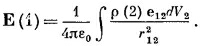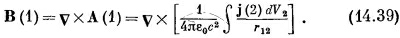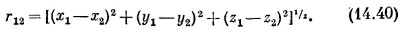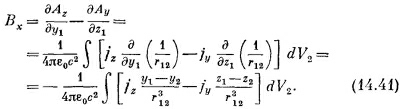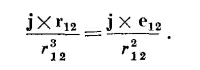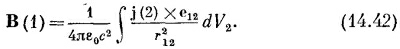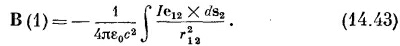| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Закон Био — Савара
В ходе изучения электростатики мы нашли, что электрическое поле известного распределения зарядов может быть получено сразу в виде интеграла [уравнение (4.16)]
Как мы видели, вычислить этот интеграл (а их на самом деле три, по одному на каждую компоненту) обычно бывает труднее, чем вычислить интеграл для потенциала и взять от него градиент.
А теперь мы должны быть осторожны. Оператор ротора означает взятие производных от А(1), т. е. он действует только на координаты (х1, y1, z1). Можно внести оператор vX под интеграл, если помнить, что он действует только на переменные со значком 1, которые появляются, конечно, только в
Мы получаем для x-компоненты В:
Величина в скобках есть просто x-компонента от
Такие же результаты получаются и для других компонент, и мы имеем
Интеграл дает В сразу через известные токи. Геометрия здесь точно такая же, какая изображена на фиг. 14.2.
(Знак минус появляется потому, что мы изменили порядок векторного произведения.) Это уравнение для В называется законом Био — Савара в честь открывших его ученых. Он дает формулу для прямого вычисления магнитного поля, создаваемого проводами с током. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.