Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 14. Магнитное поле в разных случаях Длинный соленоид
 Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным nl на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток /, и пренебрегаем небольшими зазорами между витками.) Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным nl на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток /, и пренебрегаем небольшими зазорами между витками.)
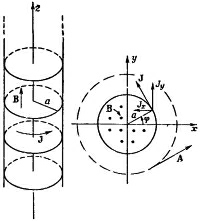
Точно так же, как мы выводили «поверхностную плотность заряда» σ, определим здесь «поверхностную плотность тока» J, равную току на единице длины по поверхности соленоида (что, конечно, есть просто среднее j, умноженное на толщину тонкой намотки). Величина J здесь равна nl. Этот поверхностный ток (фиг. 14.4) имеет компоненты
Мы должны теперь найти А для такого распределения токов.
Прежде всего найдем Ах в точках вне соленоида. Результат такой же, как электростатический потенциал вне цилиндра с поверхностным зарядом:
где σо=— J/с2. Мы не решали случай такого распределения заряда, но делали нечто похожее. Это распределение заряда эквивалентно двум жестким цилиндрам, состоящим из зарядов, один из положительных, другой из отрицательных, с малым относительным смещением их осей в направлении у. Потенциал такой пары цилиндров пропорционален производной по у от потенциала одного однородно заряженного цилиндра. Мы, конечно, можем вычислить константу пропорциональности, но пока не будем возиться с этим.
Потенциал заряженного цилиндра пропорционален In r′; потенциал пары тогда равен
Итак, мы знаем, что
где K - некоторая константа. Рассуждая точно также, найдем
Хотя мы раньше говорили, что вне соленоида магнитного поля нет, теперь мы находим, что поле А существует и циркулирует вокруг оси z (см. фиг. 14.4). Возникает вопрос: равен ли нулю его ротор?
Очевидно, Bx и By равны нулю, а
Итак, магнитное поле вне очень длинного соленоида действительно равно нулю, хотя векторный потенциал нулю не равен.
Мы можем проверить наш результат, прибегнув к другим соображениям. Циркуляция векторного потенциала вокруг соленоида должна равняться потоку В внутри катушки [уравнение (14.11)]. Циркуляция равна А·2πr′ или, поскольку А=К/r′, она равна 2πК. Заметьте, что циркуляция не зависит от r′. Так и должно быть, если В вне соленоида отсутствует, потому что поток есть просто величина В внутри соленоида, умноженная на πа2. Он один и тот же для всех окружностей с радиусом r′>а. Раньше мы нашли, что поле внутри равно nI/ε0с2, поэтому мы можем определить константу К:
Итак, векторный потенциал снаружи имеет величину
и всегда перпендикулярен вектору r′.
Мы говорили о соленоидальной катушке из проволоки, но такое же поле мы могли бы создать, вращая длинный цилиндр с электростатическим зарядом на поверхности. Если у нас есть тонкий цилиндрический слой радиуса а с поверхностным зарядом σ, то вращение цилиндра образует поверхностный ток J=σv, где v=aω — скорость поверхностного заряда. Внутри цилиндра тогда будет магнитное поле В=σаω/ε0с2.
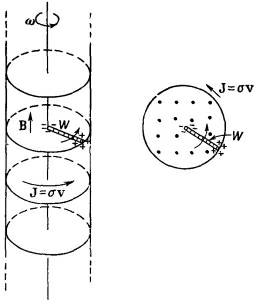 Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5). Эта проволока движется в магнитном поле, так что сила vXB приведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Е зарядов не уравновесит силы vXB). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)! Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5). Эта проволока движется в магнитном поле, так что сила vXB приведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Е зарядов не уравновесит силы vXB). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)!
Но вы, наверно, засомневаетесь: «А что, если я сам перейду,— скажете вы,— в систему координат вращающегося цилиндра? Там заряженйый цилиндр покоится, а я знаю из электростатических уравнений, что внутри цилиндра никакого поля не будет, не будет и силы, толкающей заряды к центру. Поэтому здесь что-то не так?» Нет. Все правильно, «Относительности вращения» не существует. Вращающаяся система — не инерциальная система, и законы физики в ней другие. Мы должны пользоваться уравнениями электромагнетизма только в инерциальных системах координат.
Было бы здорово, если бы смогли измерить абсолютное вращение Земли с помощью такого заряженного цилиндра, но эффект, к несчастью, настолько мал, что его невозможно наблюдать даже с помощью самых тонких современных приборов.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным nl на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток /, и пренебрегаем небольшими зазорами между витками.)
Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным nl на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток /, и пренебрегаем небольшими зазорами между витками.)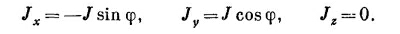
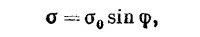
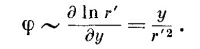


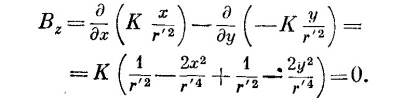
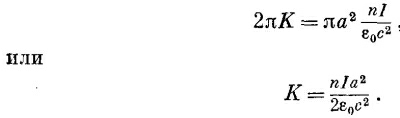

 Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5). Эта проволока движется в магнитном поле, так что сила vXB приведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Е зарядов не уравновесит силы vXB). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)!
Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5). Эта проволока движется в магнитном поле, так что сила vXB приведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Е зарядов не уравновесит силы vXB). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)!