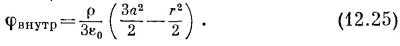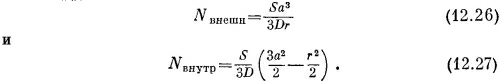| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Диффузия нейтронов. Сферически-симметричный источник в однородной среде
Приведем еще один пример, дающий уравнение того же вида, но на сей раз относящееся к диффузии. В гл. 43 (вып. 4) мы рассмотрели диффузию ионов в однородном газе и диффузию одного газа сквозь другой. Теперь возьмем другой пример — диффузию нейтронов в материале типа графита. Мы выбрали графит (разновидность чистого углерода), потому что углерод не поглощает медленных нейтронов. Нейтроны путешествуют в нем свободно. Они проходят по прямой в среднем несколько сантиметров, прежде чем рассеются ядром и отклонятся в сторону. Так что если у нас есть большой кусок графита толщиной в несколько метров, то нейтроны, находившиеся сначала в одном месте, будут переходить в другие места. Мы опишем их усредненное поведение, т. е. их средний поток.
где коэффициент диффузии D дается в терминах средней скорости ν и средней длины свободного пробега l между столкновениями:
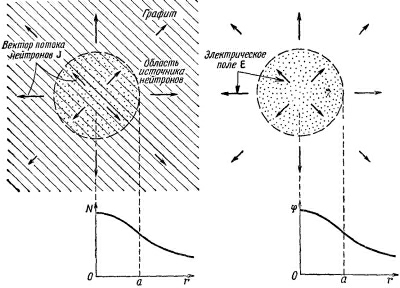
Скорость, с которой нейтроны проходят через некоторый элемент поверхности da, равна J·nda (где n, как обычно,— единичный вектор нормали). Результирующий поток из элемента объема тогда равен (пользуясь обычным гауссовым доказательством) v·JdV. Этот поток приводил бы к уменьшению числа нейтронов в ΔV, если нейтроны не генерируются внутри ΔV (с помощью какой-нибудь ядерной реакции). Если в объеме присутствуют источники, производящие S нейтронов в единицу времени в единице объема, то результирующий поток из ΔV будет равен [S—(∂Nl∂t)] ΔV. Тогда получаем
Комбинируя (12.21) и (12.20), получаем уравнение диффузии нейтронов
Для внутренних точек вклад в поле дают только заряды Q(r), находящиеся внутри сферы радиусом r; Q(r) =4πr3ρ/3, следовательно,
Поле растет линейно с r. Интегрируя Е, получаем φ:
На расстоянии радиуса а φвнешн должен совпадать с φвнутр, поэтому постоянная должна быть равна ρа2/2ε0. (Мы предполагаем, что потенциал φ равен нулю на больших расстояниях от источника, а это для нейтронов будет отвечать обращению N в нуль.) Следовательно,
Теперь мы сразу же найдем плотность нейтронов в нашей диффузионной задаче
На фиг 12.7 представлена зависимость N от r. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


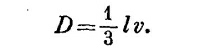

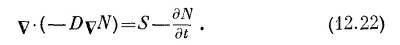
 В статическом случае, когда ∂N/∂t =0, мы снова имеем уравнение (12.4)! Мы можем воспользоваться нашими знаниями в электростатике для решения задач по диффузии нейтронов. Давайте же решим какую-нибудь задачу. (Пожалуй, вы недоумеваете: зачем решать новую задачу, если мы уже решили все задачи в электростатике? На этот раз мы можем решить быстрее именно потому, что электростатические задачи действительно уже решены!)
В статическом случае, когда ∂N/∂t =0, мы снова имеем уравнение (12.4)! Мы можем воспользоваться нашими знаниями в электростатике для решения задач по диффузии нейтронов. Давайте же решим какую-нибудь задачу. (Пожалуй, вы недоумеваете: зачем решать новую задачу, если мы уже решили все задачи в электростатике? На этот раз мы можем решить быстрее именно потому, что электростатические задачи действительно уже решены!)