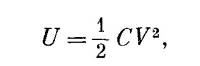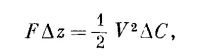| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Энергия конденсатора. Силы. действующие на заряженные проводники
Рассмотрим теперь энергию, требуемую на то, чтоб зарядить конденсатор. Если заряд Q был снят с одной обкладки конденсатора и перенесен на другую, то между обкладками возникает разность потенциалов, равная
где С — емкость конденсатора. Сколько работы затрачено на зарядку конденсатора? Поступая точно так же, как мы поступали с шаром, вообразим, что конденсатор уже заряжен переносом заряда с одной обкладки на другую маленькими порциями dQ. Работа, требуемая для переноса заряда dQ, равна
Взяв V из (8.8), напишем
Или, интегрируя от Q = 0 до конечного заряда Q, получаем
Эту энергию можно также записать в виде
Вспоминая, что емкость проводящей сферы (по отношению к бесконечности) равна
мы немедленно получим из уравнения (8.9) энергию заряженной сферы
Это выражение, конечно, относится также и к энергии тонкого сферического слоя с полным зарядом Q; получается 5/6 энергии однородно заряженного шара [уравнение (8.7)].
где F — сила, действующая между обкладками. Эта работа обязана быть равной изменению электростатической энергии конденсатора, если только заряд конденсатора не изменился.
Изменение в энергии (если мы не допускаем изменения величины заряда) тогда равно
Приравнивая (8.12) и (8.13), получаем
что может также быть записано в виде
Ясно, эта сила здесь возникает от притяжения зарядов на обкладках; мы видим, однако,что заботиться о том, как там они распределены, нам нечего; единственное, что нам нужно,— это учесть емкость С.
где А — площадь каждой обкладки. Если промежуток увеличится на Δz, то
Из (8.14) тогда следует, что сила притяжения между двумя обкладками равна
Взглянем на уравнение (8.17) повнимательнее и подумаем, нельзя ли сказать, как возникает эта сила. Если заряд на одной из обкладок мы запишем в виде
то (8.17) можно будет переписать так:
поскольку поле между пластинами равно
Вы должны обратить внимание на то, что, рассчитывая виртуальную работу, мы предположили, что заряд конденсатора постоянен, что конденсатор не был электрически связан с другими предметами и полный заряд не мог изменяться.
и вместо (8.15) мы бы имели
что приводит к силе, равной по величине той, что была получена в уравнении (8.15) (так как V=Q/C), но с противоположным знаком! СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


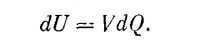
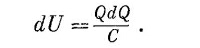


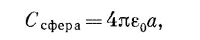


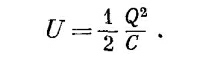
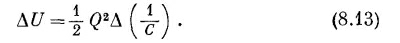
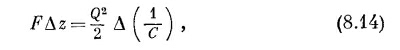

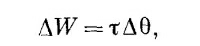
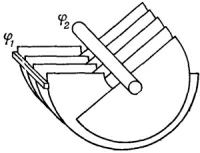 где Δθ — небольшой угловой поворот. Конечно, теперь Δ(1/С) должно быть изменением 1/С, отвечающим повороту на Δθ. Таким способом мы можем определить вращательный момент, действующий на подвижные пластины переменного конденсатора, показанного на фиг. 8.3.
где Δθ — небольшой угловой поворот. Конечно, теперь Δ(1/С) должно быть изменением 1/С, отвечающим повороту на Δθ. Таким способом мы можем определить вращательный момент, действующий на подвижные пластины переменного конденсатора, показанного на фиг. 8.3.
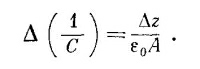

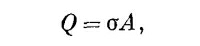
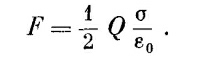
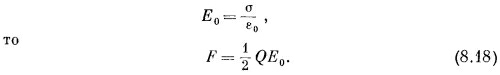
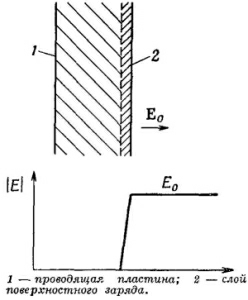 Можно было сразу догадаться, что сила, действующая на одну из пластин, будет равна заряду Q этой пластины, умноженному на поле, действующее на заряд. Но что удивляет, так это множитель 1/2. Дело в том, что Е0 —это не то поле, которое действует на заряды. Если вообразить, что заряд на поверхности пластины занимает какой-то тонкий слой (фиг. 8.4), то поле будет меняться от нуля на внутренней границе слоя до Е0 в пространстве снаружи пластин. Среднее поле, действующее на поверхностные заряды, равно E0/2. Вот отчего в (8.18) стоит множитель 1/2.
Можно было сразу догадаться, что сила, действующая на одну из пластин, будет равна заряду Q этой пластины, умноженному на поле, действующее на заряд. Но что удивляет, так это множитель 1/2. Дело в том, что Е0 —это не то поле, которое действует на заряды. Если вообразить, что заряд на поверхности пластины занимает какой-то тонкий слой (фиг. 8.4), то поле будет меняться от нуля на внутренней границе слоя до Е0 в пространстве снаружи пластин. Среднее поле, действующее на поверхностные заряды, равно E0/2. Вот отчего в (8.18) стоит множитель 1/2.