| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Двумерные поля; функции комплексного переменного
Комплексная величина з определяется так:
(Не перепутайте з с координатой z; координата z не встретится в дальнейшем, потому что зависимости полей от z не будет.) Тогда каждой точке на плоскости (х, у) отвечает комплексное число з. Мы можем считать з особой (комплексной) переменной величиной и с ее помощью записывать обычные математические функции F(з). Например,
и т. д.
Любую функцию F (з) можно записать в виде суммы чисто действительной и чисто мнимой частей, и каждая из частей будет функцией от х и у:
где U(x, у) и V(x, у) — действительные функции. Значит, из любой комплексной функции F(з) можно произвести две новые функции U (х, у) и V(x, у). К примеру, F(з)=з2 дает две функции:
Мы подошли сейчас к удивительной математической теореме, столь прекрасной, что доказательство ее придется отложить до соответствующего математического курса. (Если мы начнем заранее приоткрывать все тайны математики, она покажется вам потом скучной.) Теорема эта состоит вот в чем. Для любой «нормальной» функции U и V автоматически удовлетворяют соотношениям
Отсюда немедленно следует, что каждая из функций U и V удовлетворяет уравнению Лапласа:
Сразу видно, что для функций (7.5) и (7.6) эти уравнения выполняются.
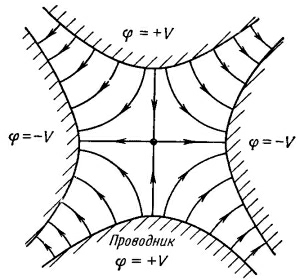
Найденное нами решение отвечает также гиперболическому электроду, помещенному около прямого угла, или двум гиперболам при соответствующих потенциалах. Заметьте, что поле фиг. 7.1 имеет интересное свойство. Составляющая х электрического поля Е дается выражением
Если мы напишем
откуда следует
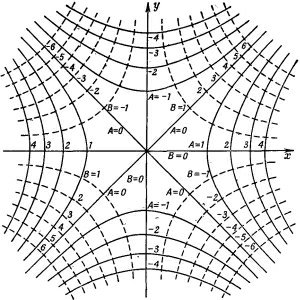
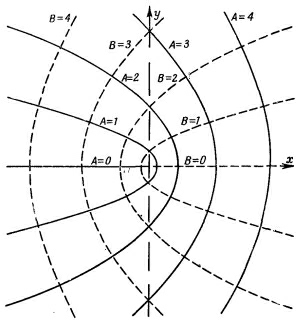
Кривые U (х, у) =А и V(x, у)=В, где U и V взяты из уравнения (7.12), проведены на фиг. 7.4. И здесь тоже можно назвать немало случаев, описываемых этими полями.
дающая нам поле снаружи прямого угла, функция
дающая поле заряженной нити, и функция
изображающая поле двумерного аналога электрического диполя, т. е. двух параллельных прямых, заряженных противоположным знаком и помещенных вплотную друг к другу. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

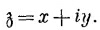

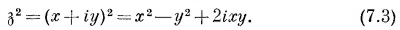
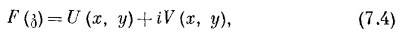
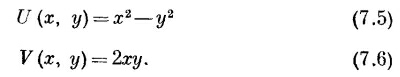
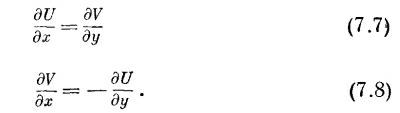

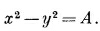
 Это уравнение прямоугольной гиперболы. Перебирая разные значения А, мы получаем семейство гипербол, начерченное на фиг. 7.1. Когда А=0, то гиперболы вырождаются в пару диагоналей, проходящих через начало.
Это уравнение прямоугольной гиперболы. Перебирая разные значения А, мы получаем семейство гипербол, начерченное на фиг. 7.1. Когда А=0, то гиперболы вырождаются в пару диагоналей, проходящих через начало.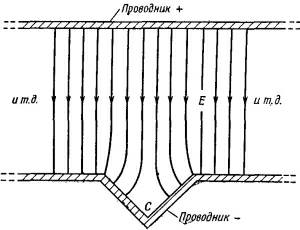 Такое семейство эквипотенциальных поверхностей встречается в нескольких физических задачах. В одной из них оно изображает детали структуры поля возле точки между двумя одинаковыми точечными зарядами. В другой оно изображает поле внутри прямого угла, образованного двумя проводящими плоскостями. Если есть два электрода, изогнутых так, как показано на фиг. 7.2, и имеющих разные потенциалы, то поле внутри угла С будет выглядеть в точности так же, как поле около начала координат на фиг. 7.1. Сплошные линии — это эквипотенциальные поверхности, а пересекающие их штриховые — это линии поля Е. Вблизи острия или выступа электрическое поле повышается, а возле впадины или отверстия оно слабеет.
Такое семейство эквипотенциальных поверхностей встречается в нескольких физических задачах. В одной из них оно изображает детали структуры поля возле точки между двумя одинаковыми точечными зарядами. В другой оно изображает поле внутри прямого угла, образованного двумя проводящими плоскостями. Если есть два электрода, изогнутых так, как показано на фиг. 7.2, и имеющих разные потенциалы, то поле внутри угла С будет выглядеть в точности так же, как поле около начала координат на фиг. 7.1. Сплошные линии — это эквипотенциальные поверхности, а пересекающие их штриховые — это линии поля Е. Вблизи острия или выступа электрическое поле повышается, а возле впадины или отверстия оно слабеет.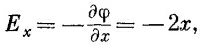
 т. е. электрическое поле пропорционально расстоянию от оси координат. Этот факт был использован, чтобы создать устройство (называемое квадрупольной линзой), необходимое для фокусирования пучков частиц (см. вып. 6, гл. 29, § 9). Фокусирующее поле обычно получают с помощью четырех гиперболических электродов, изображенных на фиг. 7.3. Проводя здесь линии электрического поля, мы просто перечертили с фиг. 7.1 семейство штриховых кривых V=const. Эти линии достались нам совершенно бесплатно! Кривые V=const перпендикулярны к кривым U=const, как это следует из уравнений (7.7) и (7.8). Как только мы выбираем функцию F(з), то получаем из U и V сразу же эквипотенциальные линии и линии поля. Мы давно знаем, что можно решить на выбор любую из двух задач, смотря по тому, какое семейство кривых мы примем за эквипотенциальное.
т. е. электрическое поле пропорционально расстоянию от оси координат. Этот факт был использован, чтобы создать устройство (называемое квадрупольной линзой), необходимое для фокусирования пучков частиц (см. вып. 6, гл. 29, § 9). Фокусирующее поле обычно получают с помощью четырех гиперболических электродов, изображенных на фиг. 7.3. Проводя здесь линии электрического поля, мы просто перечертили с фиг. 7.1 семейство штриховых кривых V=const. Эти линии достались нам совершенно бесплатно! Кривые V=const перпендикулярны к кривым U=const, как это следует из уравнений (7.7) и (7.8). Как только мы выбираем функцию F(з), то получаем из U и V сразу же эквипотенциальные линии и линии поля. Мы давно знаем, что можно решить на выбор любую из двух задач, смотря по тому, какое семейство кривых мы примем за эквипотенциальное.
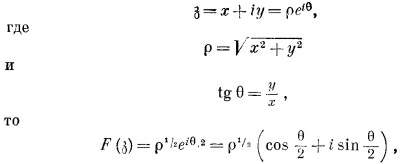
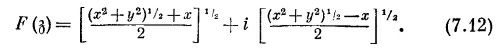
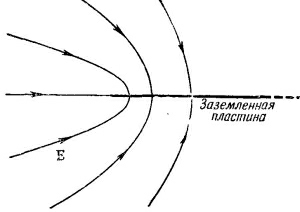 Один из самых интересных — это поле у края тонкой пластинки. Если линия B=0 направо от оси у изображает тонкую заряженную пластину, то линии поля близ нее даются кривыми с различными А. Физическая картина показана на фиг. 7.5.
Один из самых интересных — это поле у края тонкой пластинки. Если линия B=0 направо от оси у изображает тонкую заряженную пластину, то линии поля близ нее даются кривыми с различными А. Физическая картина показана на фиг. 7.5.