| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Электрический диполь
Мы не собираемся выписывать формулу для электрического поля, но всегда при желании можем это сделать, раз мы знаем потенциал. Так что задача двух зарядов решена.
Взглянем теперь на поле двух зарядов противоположных знаков, расстояние d между которыми мало. Если d станет нулем, два заряда сойдутся в одном месте, два потенциала сократятся, поле исчезнет. Но если они не совсем слились, то можно получить хорошее приближение к потенциалу, разложив слагаемые в (6.8) в ряд по степеням малой величины d (по формуле бинома Ньютона). Оставляя только первые степени d, мы напишем
Удобно обозначить
Тогда
Разлагая в биномиальный ряд [1 – (zd/r2)] -1/2 и отбрасывая члены с высшими степенями d, мы получаем
Подобно этому, и
Вычитая эти два члена, имеем для потенциала
Потенциал, а значит, и поле, являющееся его производной, пропорциональны qd — произведению заряда на расстояния между зарядами. Это произведение называется диполъным моментом пары зарядов, и мы обозначим его символом р (не путайте с импульсом!):
Уравнение (6.9) можно также записать в виде
так как z/r=cos θ, где θ — угол между осью диполя и радиус-вектором к точке (х, у, z) (см. фиг. 6.1). Потенциал диполя убывает как 1/r2 при фиксированном направлении (а у точечного заряда он убывает как 1/r). Электрическое поле Е диполя поэтому убывает как 1/r3.
Эта формула справедлива для диполя произвольной ориентации и положения, если r — вектор, направленный от диполя к интересующей нас точке.
или
А х- и y-компоненты равны
Из этих двух компонент можно составить компоненту, перпендикулярную к оси z, которая называется поперечной компонентой Еι:
Поперечная компонента Eι лежит в плоскости ху и направлена прямо от оси диполя. Полное поле, конечно, равно
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

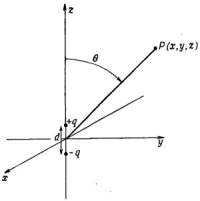 Сначала возьмем два точечных заряда +q и –q, разделенных промежутком d. Проведем ось z через заряды, а начало координат поместим посредине между ними (фиг. 6.1). Тогда по формуле (4.24) потенциал системы двух зарядов дается выражением
Сначала возьмем два точечных заряда +q и –q, разделенных промежутком d. Проведем ось z через заряды, а начало координат поместим посредине между ними (фиг. 6.1). Тогда по формуле (4.24) потенциал системы двух зарядов дается выражением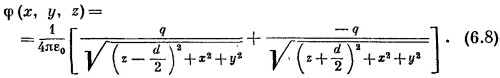
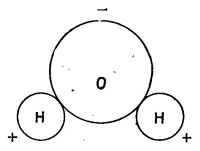 В некоторых молекулах из-за самой их формы заряды несколько разделены даже в отсутствие внешних полей. В молекуле воды, например, имеется отрицательный заряд на атоме кислорода и положительный заряд на обоих атомах водорода, которые расположены несимметрично (фиг. 6.2). Хоть заряд всей молекулы равен нулю, все же имеется распределение заряда с небольшим преобладанием отрицательного заряда на одной стороне и положительного на другой. Это расположение, конечно, не такое простое, как у двух точечных зарядов, но если смотреть на него издалека, оно действует как диполь. Как мы увидим чуть позже, поле на больших расстояниях нечувствительно к мелким деталям расположения.
В некоторых молекулах из-за самой их формы заряды несколько разделены даже в отсутствие внешних полей. В молекуле воды, например, имеется отрицательный заряд на атоме кислорода и положительный заряд на обоих атомах водорода, которые расположены несимметрично (фиг. 6.2). Хоть заряд всей молекулы равен нулю, все же имеется распределение заряда с небольшим преобладанием отрицательного заряда на одной стороне и положительного на другой. Это расположение, конечно, не такое простое, как у двух точечных зарядов, но если смотреть на него издалека, оно действует как диполь. Как мы увидим чуть позже, поле на больших расстояниях нечувствительно к мелким деталям расположения.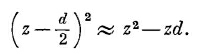
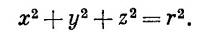
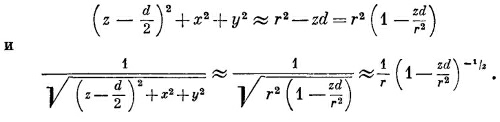
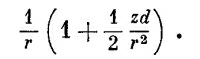
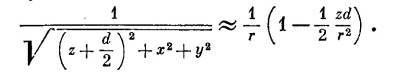
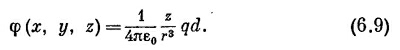

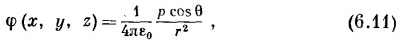

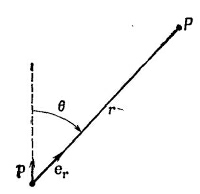 где еr— единичный радиальный вектор (фиг. 6.3). Кроме того, точку (х, у, z) можно обозначить буквой r. Итак,
где еr— единичный радиальный вектор (фиг. 6.3). Кроме того, точку (х, у, z) можно обозначить буквой r. Итак,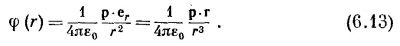
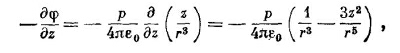
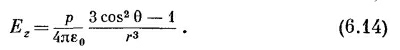
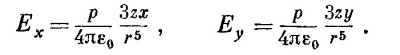
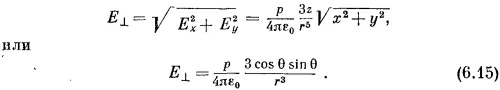
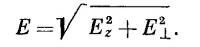
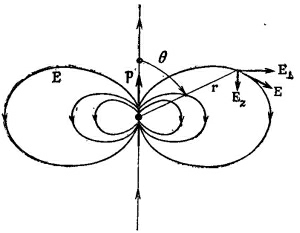 Поле диполя меняется обратно пропорционально кубу расстояния от диполя. На оси при θ =0 оно вдвое сильнее, чем при θ =90°. При обоих этих углах электрическое поле обладает только z-компонентой. Знаки ее при z=0 и при z=90° противоположны (фиг. 6.4).
Поле диполя меняется обратно пропорционально кубу расстояния от диполя. На оси при θ =0 оно вдвое сильнее, чем при θ =90°. При обоих этих углах электрическое поле обладает только z-компонентой. Знаки ее при z=0 и при z=90° противоположны (фиг. 6.4).