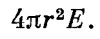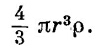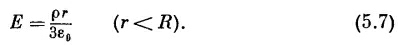| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Однородно заряженный шар; заряженная сфера
В гл. 4 мы уже применяли закон Гаусса, когда должны были найти поле вне однородно заряженной шаровой области. Тот же метод может дать нам и поле в точках внутри шара. Этот расчет, например, может быть использован для получения хорошего приближения к полю внутри атомного ядра. Вопреки тому, что протоны в ядре взаимно отталкиваются, они из-за сильного ядерного притяжения распределены по всему ядру почти однородно.
Заряд внутри нее равен внутреннему объему, умноженному на ρ, т. е.
Применяя закон Гаусса, получаем величину поля
Вы видите, что при r=R эта формула дает правильный результат. Электрическое поле пропорционально расстоянию от центра и направлено по радиусу наружу. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

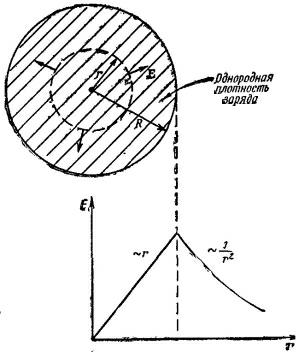 Пусть у нас имеется сфера радиуса R, однородно наполненная зарядами. Пусть заряд в единице объема равен ρ. Снова, используя соображения симметрии, можно предположить, что поле радиально и в точках, равноудаленных от центра, по величине одинаково. Чтоб определить поле в точке на расстоянии r от центра, представим сферическую гауссову поверхность радиуса r (r<R), как показано на фиг. 5.8. Поток из нее равен
Пусть у нас имеется сфера радиуса R, однородно наполненная зарядами. Пусть заряд в единице объема равен ρ. Снова, используя соображения симметрии, можно предположить, что поле радиально и в точках, равноудаленных от центра, по величине одинаково. Чтоб определить поле в точке на расстоянии r от центра, представим сферическую гауссову поверхность радиуса r (r<R), как показано на фиг. 5.8. Поток из нее равен