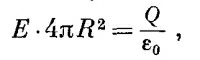| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Поле заряженного шара
Одной из самых трудных задач, которую пришлось нам решать, когда мы изучали теорию гравитационного притяжения, было доказать, что сила, создаваемая твердым шаром на его поверхности, такая же, как если бы все вещество шара было сконцентрировано в его центре. Много лет Ньютон не решался обнародовать свою теорию тяготения, так как не был уверен в правильности этой теоремы. Мы доказали ее в вып. 1, гл. 13, взяв интеграл для потенциала и вычислив силу тяготения по градиенту. Теперь эту теорему мы можем доказать очень просто. Но на этот раз мы докажем не совсем ее, а сходную теорему для однородно заряженного электричеством шара. (Поскольку законы электростатики и тяготения совпадают, то то же доказательство может быть проведено и для поля тяготения.)
Закон Гаусса утверждает, что этот поток равен суммарному заряду сферы Q (деленному на ε0):
или
а это как раз та формула, которая получилась бы для точечного заряда Q. Мы решили проблему Ньютона проще, без интеграла. Конечно, это кажущаяся простота; вам пришлось затратить какое-то время на то, чтобы разобраться в законе Гаусса, и вы можете думать, что на самом деле время нисколько не сэкономлено. Но когда вам придется часто применять эту теорему, то она практически окупится. Все дело в привычке. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

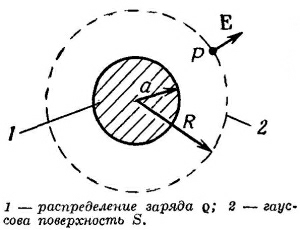 Зададим вопрос: каково электрическое поле Е в точке Р где-то снаружи сферы, наполненной однородно распределенным зарядом?Так как здесь нет «выделенного» направления, то законно допустить, что Е всюду направлено прямо от центра сферы. Рассмотрим воображаемую сферическую поверхность, концентрическую со сферой зарядов и проходящую через точку Р (фиг. 4.11). Для этой сферы поток наружу равен
Зададим вопрос: каково электрическое поле Е в точке Р где-то снаружи сферы, наполненной однородно распределенным зарядом?Так как здесь нет «выделенного» направления, то законно допустить, что Е всюду направлено прямо от центра сферы. Рассмотрим воображаемую сферическую поверхность, концентрическую со сферой зарядов и проходящую через точку Р (фиг. 4.11). Для этой сферы поток наружу равен