| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Циркуляция векторного поля
Мы хотим теперь рассмотреть ротор доля примерно так же, как рассматривали дивергенцию. Мы вывели теорему Гаусса, вычисляя интеграл по поверхности, хотя с самого начала отнюдь не было ясно, что мы будем иметь дело с дивергенцией. Откуда же можно было знать, что для ее получения надо интегрировать по поверхности? Этот результат вовсе не был очевиден. И столь же неоправданно мы сейчас вычислим другую характеристику поля и покажем, что она связана с ротором. На этот раз мы подсчитаем так называемую циркуляцию векторного поля. Если С — произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру. Мы уже раньте в этой главе рассматривали криволинейный интеграл от vψ. Сейчас мы то же самое проделываем с произвольным векторным полем С.
Заметьте, что интеграл берется по всему замкнутому пути, а не от одной точки до другой, как это делалось раньше. Кружочек на знаке интеграла должен нам напоминать об этом. Такой интеграл называется циркуляцией векторного поля по кривой Г. Название связано с тем, что первоначально так рассчитывали циркуляцию жидкости. Но название это, как и поток, было распространено на любые поля, даже такие, в которых «циркулировать» нечему.
Циркуляция вдоль Г1 есть сумма интеграла вдоль Га и вдоль ГаЬ. Точно так же и циркуляция вдоль Г2 есть сумма двух частей, одной вдоль Гb, другой — вдоль ГаЬ. Интеграл вдоль ГаЬ для кривой Г2 имеет знак, противоположный тому знаку, который он имел для кривой Г1 потому что направления обхода противоположны (в обоих криволинейных интегралах направления поворота нужно брать одни и те же).
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2024
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

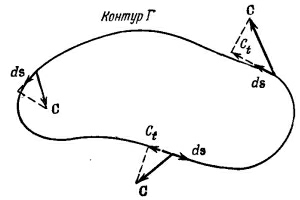 Пусть Г — произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на фиг. 3.7. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде
Пусть Г — произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на фиг. 3.7. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде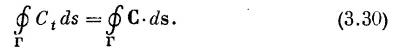
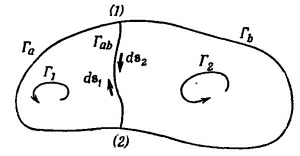 Забавляясь той же игрой, как с потоком, мы можем показать, что циркуляция вдоль контура есть сумма циркуляции вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г1 и Г2 (фиг. 3.8). Контур Г1 состоит из Га — части первоначальной кривой слева от (1) и (2) и «соединения» ГаЬ. Контур Г2 состоит из остатка первоначальной кривой плюс то же соединение.
Забавляясь той же игрой, как с потоком, мы можем показать, что циркуляция вдоль контура есть сумма циркуляции вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г1 и Г2 (фиг. 3.8). Контур Г1 состоит из Га — части первоначальной кривой слева от (1) и (2) и «соединения» ГаЬ. Контур Г2 состоит из остатка первоначальной кривой плюс то же соединение.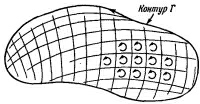 Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное множество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зависят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (фиг. 3.9). Какой бы ни была форма поверхности, но если малые контуры сделать достаточно малыми, всегда можно будет считать каждый из них замыкающим достаточно плоскую поверхность. Кроме того, каждый из них можно сделать очень похожим на квадрат. И циркуляцию вокруг большого контура Г можно найти, подсчитав циркуляции по всем квадратикам и сложив их.
Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное множество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зависят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (фиг. 3.9). Какой бы ни была форма поверхности, но если малые контуры сделать достаточно малыми, всегда можно будет считать каждый из них замыкающим достаточно плоскую поверхность. Кроме того, каждый из них можно сделать очень похожим на квадрат. И циркуляцию вокруг большого контура Г можно найти, подсчитав циркуляции по всем квадратикам и сложив их.