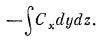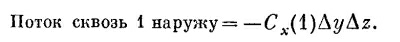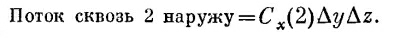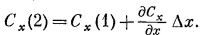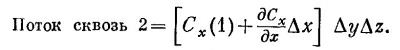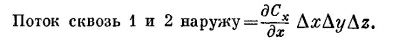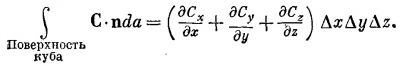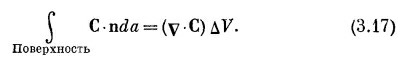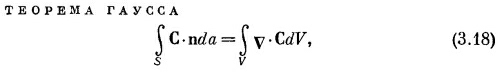| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Поток из куба; теорема Гаусса
Так как куб считается малым, этот интеграл можно заменить значением Сх в центре грани [эту точку мы обозначили (1)], умноженным на площадь грани ΔyΔz:
Подобным же образом поток наружу через грань 2 равен
Величины Сх(1) и Сх(2), вообще говоря, слегка отличаются. Если Δx достаточно мало, то можно написать
Существуют, конечно, и другие члены, но в них входит (Δx)2 и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
Складывая потоки через грани 1 и 2, получаем
Производную нужно вычислять в центре грани 1, т. е. в точке [х, y + (Δy/2), z+(Δz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
Сумма производных в скобках как раз есть v·С, a ΔxΔyΔz=ΔV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р.
где S — произвольная замкнутая поверхность, V — объем внутри нее. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

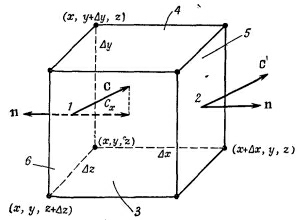 Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен
Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен