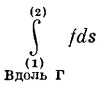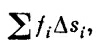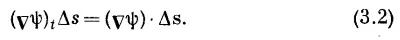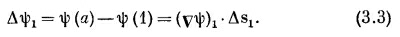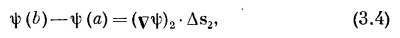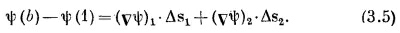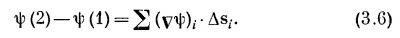| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Векторные интегралы; криволинейный интеграл от V Ψ
В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено довольно много, все их можно подытожить одним правилом: операторы д/дх, д/ду и дlдz суть три компоненты векторного оператора v. Сейчас нам хотелось бы лучше разобраться в значении производных поля. Тогда мы легче почувствуем смысл векторных уравнений поля.
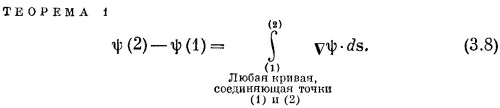
Интеграл, стоящий здесь, это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора vψ на другой вектор, ds, являющийся бесконечно малым элементом дуги кривой Г [направленной от (1) к (2)].
подразумевается предел суммы
где f¡ — значение функции где-то на ¡-й хорде. Предел — это то, к чему стремится сумма, когда растет число хорд (разумным образом, чтобы даже наибольшее Δs¡ →0).
Интеграл в (3.1) и подразумевает сумму таких членов.
Точно так же мы имеем
где, конечно, (vψ)1 означает градиент, вычисленный на хорде Δs1, а (vψ)2 — градиент, вычисленный на Δs2. Сложив (3.3) и (3.4), получим
Вы видите, что, продолжая прибавлять такие члены, мы получаем в итоге
Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как равенство не зависит и от выбора точек а,b, с,..., точно так же оно не зависит от выбора самой кривой Г. Теорема верна для любой кривой, соединяющей точки (1) и (2).
Тогда наша теорема примет такой вид:
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

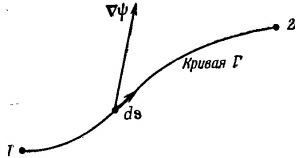 Мы начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ψ(x, у, z). В двух произвольных точках (1) и (2) функция ψ имеет соответственно значения ψ(1) и ψ(2). (Используется такое удобное обозначение: (2) означает точку (х2, у2, z2), а ψ(2) это то же самое, что ψ(x2, y2, z2).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива
Мы начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ψ(x, у, z). В двух произвольных точках (1) и (2) функция ψ имеет соответственно значения ψ(1) и ψ(2). (Используется такое удобное обозначение: (2) означает точку (х2, у2, z2), а ψ(2) это то же самое, что ψ(x2, y2, z2).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива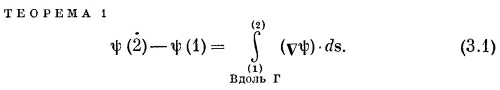
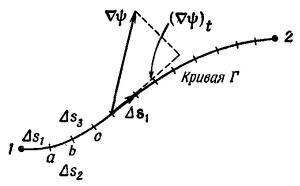 Напомним, что мы понимаем под криволинейным интегралом. Рассмотрим скалярную функцию f (х, у, z) и кривую Г, соединяющую две точки (1) и (2). Отметим на кривой множество точек и соединим их хордами, как на фиг. 3.2. Длина ¡-й хорды равна Δs¡, где ¡ пробегает значения 1, 2, 3,... . Под криволинейным интегралом
Напомним, что мы понимаем под криволинейным интегралом. Рассмотрим скалярную функцию f (х, у, z) и кривую Г, соединяющую две точки (1) и (2). Отметим на кривой множество точек и соединим их хордами, как на фиг. 3.2. Длина ¡-й хорды равна Δs¡, где ¡ пробегает значения 1, 2, 3,... . Под криволинейным интегралом