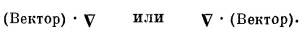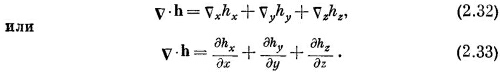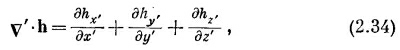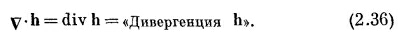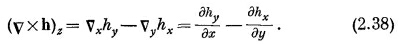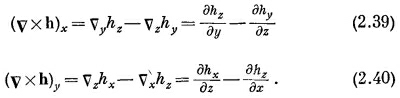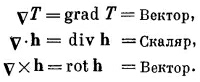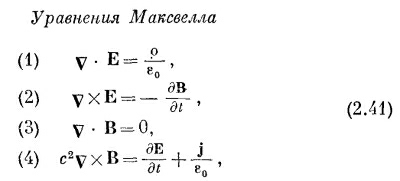| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Операция с V
Можно ли с векторным оператором v производить другие алгебраические действия? Попробуем скомбинировать его с вектором. Из двух векторов можно составить скалярное произведение, причем двоякого рода:
Первое выражение пока что ничего не означает — это все еще оператор. Окончательный смысл его зависит от того, на что он будет действовать. А второе произведение — это некое скалярное поле (потому что А·В — всегда скаляр).
Эта сумма инвариантна относительно преобразования координат. Если выбрать другую систему (отмеченную штрихами), то получилось бы
а это — то же самое число, которое получилось бы и из (2.33), хотя с виду оно выглядит иначе, т. е.
в любой точке пространства. Итак, v·h — это скалярное поле, и оно должно представить собой некоторую физическую величину. Вы должны понимать, что комбинация производных в v·h имеет довольно специальный вид. Могут быть и другие комбинации всяческого вида, скажем дhy /дх, которые не являются ни скалярами, ни компонентами векторов.
Можно было бы, как и для vТ, описать физический смысл v·h. Но мы отложим это до лучших времен.
Компоненты этого вектора можно написать, пользуясь обычным правилом для векторного произведения [см. (2.2)]:
Подобно этому,
Комбинацию v x h называют «ротор» (пишут rot h), или (редко) «вихрь h» (пишут curl h). Происхождение этого названия и физический смысл комбинации мы обсудим позже.
Используя эти комбинации, можно пространственные вариации полей записывать в удобном виде, т. е. в виде, не зависящем от той или иной совокупности осей координат.
где ρ (po) — «плотность электрического заряда» (количество заряда в единице объема), a j — «плотность электрического тока» (скорость протекания заряда сквозь единицу площади). Эти четыре уравнения содержат в себе законченную классическую теорию электромагнитного поля. Видите, какой элегантной и простой записи мы добились с помощью наших новых обозначений! СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.