| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Скалярные и векторные поля — T и h
Мы начинаем сейчас рассмотрение абстрактного, математического подхода к теории электричества и магнетизма. Наша цель — объяснить смысл законов, написанных в гл. 1. Но для этого надо сперва объяснить новые особенные обозначения, которые мы хотим использовать. Давайте поэтому на время позабудем электромагнетизм и разберемся в математике векторных полей. Она очень важна не только в электромагнетизме, но и во многих физических обстоятельствах, подобно тому как обычное дифференциальное и интегральное исчисление важно во всех областях физики. Мы переходим к дифференциальному исчислению векторов.
Мы будем также пользоваться следующими двумя равенствами:
Уравнение (2.7) справедливо, конечно, только при Δх, Δy и Δz→0.
где еf — единичный вектор направления потока.
Поясним это уравнение: поток тепла (в единицу времени и на единицу площади) через произвольный элемент поверхности с единичной нормалью n равен h·n. Можно еще сказать так: компонента потока тепла, перпендикулярная к элементу поверхности Δа2, равна h·n. Можно, если мы хотим, считать эти утверждения определением h. Сходные идеи мы применим и к другим векторным полям. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

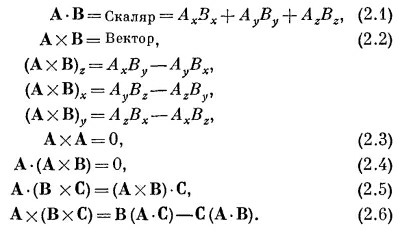
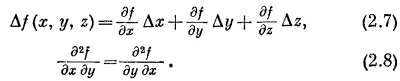
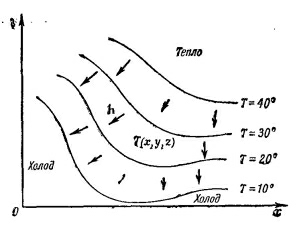 Один способ представить себе скалярное поле — это вообразить «контуры», т. е. мысленные поверхности, проведенные через точки с одинаковыми значениями поля, подобно горизонталям на картах, соединяющим точки на одной высоте над уровнем моря. Для температурного поля контуры носят название «изотермические поверхности», или изотермы. На фиг. 2.1 показано температурное поле и зависимость Т от х и у при z=0. Проведено несколько изотерм.
Один способ представить себе скалярное поле — это вообразить «контуры», т. е. мысленные поверхности, проведенные через точки с одинаковыми значениями поля, подобно горизонталям на картах, соединяющим точки на одной высоте над уровнем моря. Для температурного поля контуры носят название «изотермические поверхности», или изотермы. На фиг. 2.1 показано температурное поле и зависимость Т от х и у при z=0. Проведено несколько изотерм.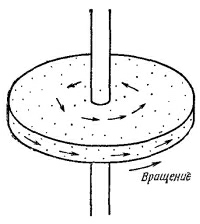 Поля бывают также векторными. Идея их очень проста. В каждой точке пространства задается вектор. Он меняется от точки к точке. Рассмотрим в виде примера вращающееся тело. Скорость материала тела во всякой точке — это вектор, который является функцией ее положения (фиг. 2.2). Другой пример — поток тепла в бруске из некоторого материала. Если в одной части бруска температура выше, а в другой — ниже, то от горячей части к холодной будет идти поток тепла. Тепло в разных частях бруска будет растекаться в различных направлениях. Поток тепла — это величина, имеющая направление; обозначим ее h; длина этого вектора пусть измеряет количество протекающего тепла. Векторы потока тепла также изображены на фиг. 2.1.
Поля бывают также векторными. Идея их очень проста. В каждой точке пространства задается вектор. Он меняется от точки к точке. Рассмотрим в виде примера вращающееся тело. Скорость материала тела во всякой точке — это вектор, который является функцией ее положения (фиг. 2.2). Другой пример — поток тепла в бруске из некоторого материала. Если в одной части бруска температура выше, а в другой — ниже, то от горячей части к холодной будет идти поток тепла. Тепло в разных частях бруска будет растекаться в различных направлениях. Поток тепла — это величина, имеющая направление; обозначим ее h; длина этого вектора пусть измеряет количество протекающего тепла. Векторы потока тепла также изображены на фиг. 2.1.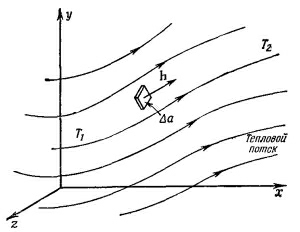 Определим теперь h более точно. Длина вектора потока тепла в данной точке — это количество тепловой энергии, проходящее за единицу времени и в пересчете на единицу площади сквозь бесконечно малый элемент поверхности, перпендикулярный к направлению потока. Вектор указывает направление потока (фиг. 2.3). В буквенных обозначениях: если ΔJ — тепловая энергия, протекающая за единицу времени сквозь элемент поверхности Δа, то
Определим теперь h более точно. Длина вектора потока тепла в данной точке — это количество тепловой энергии, проходящее за единицу времени и в пересчете на единицу площади сквозь бесконечно малый элемент поверхности, перпендикулярный к направлению потока. Вектор указывает направление потока (фиг. 2.3). В буквенных обозначениях: если ΔJ — тепловая энергия, протекающая за единицу времени сквозь элемент поверхности Δа, то
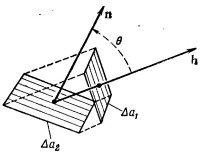 Вектор h можно определить и иначе — через его компоненты. Зададим себе вопрос, сколько тепла протекает через малую поверхность под произвольным углом к направлению потока. На фиг. 2.4 мы изобразили малую поверхность Δа2 под некоторым углом к поверхности Δа1, которая перпендикулярна к потоку. Единичный вектор n перпендикулярен к поверхности Δа2. Угол θ между n и h равен углу между поверхностями (так как h — нормаль к Δа1). Чему теперь равен поток тепла через Δа2 на единицу площади? Потоки сквозь Δа2 и Δа1 равны между собой, отличаются только площади. Действительно, Δа1 = Δа2 cos θ. Поток тепла через Δа2 равен
Вектор h можно определить и иначе — через его компоненты. Зададим себе вопрос, сколько тепла протекает через малую поверхность под произвольным углом к направлению потока. На фиг. 2.4 мы изобразили малую поверхность Δа2 под некоторым углом к поверхности Δа1, которая перпендикулярна к потоку. Единичный вектор n перпендикулярен к поверхности Δа2. Угол θ между n и h равен углу между поверхностями (так как h — нормаль к Δа1). Чему теперь равен поток тепла через Δа2 на единицу площади? Потоки сквозь Δа2 и Δа1 равны между собой, отличаются только площади. Действительно, Δа1 = Δа2 cos θ. Поток тепла через Δа2 равен