| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Большие расстояния
Вернемся теперь к вопросу о расстоянии. Как далеко отстоят от нас окружающие предметы и как велики они? Всем известно, что для измерения расстояния нужно взять какую-то единицу длины и считать, сколько этих единиц укладывается на данном отрезке. Но как измерить те предметы, которые меньше единицы длины? Как подразделить выбранную единицу длины? А точно так же, как и время: мы берем меньшую единицу длины и считаем, сколько таких единиц укладывается в большей. Таким методом мы сможем измерять все меньшие и меньшие длины.
В последний год достигнуты большие успехи в определении масштаба солнечной системы. В Лаборатории ракетных двигателей с помощью прямой радиолокационной связи были проведены очень точные измерения расстояния от Земли до Венеры. Здесь мы имеем дело еще с одним определением понятия «расстояние». Нам известна скорость распространения света (а стало быть, и скорость распространения радиоволн), и мы предполагаем, что эта скорость постоянна на всем протяжении между Землей и Венерой. Послав радиоволну по направлению к Венере, мы считаем время до прихода обратно отраженной волны. А зная время и скорость, мы получаем расстояние.
Изучение многих шаровых скоплений дает еще одну важную информацию. Оказалось, что существует участок неба с большой концентрацией таких шаровых скоплений, причем большинство из них находится на одном и том же расстоянии от нас. Сравнивая эти данные с некоторыми другими, мы приходим к заключению, что эти скопления являются центром нашей Галактики. Таким образом мы определяем, что расстояние до центра Галактики составляет приблизительно 1020 м. Данные о размере нашей Галактики дают ключ к определению еще больших межгалактических расстояний. На фиг. 5.7 приведена фотография галактики, которая по форме очень похожа на нашу Галактику. Возможно, что и размер ее тот же. (Есть еще ряд соображений, согласно которым размеры всех галактик приблизительно одинаковы.) А если это так, то можно узнать расстояние до нее. Мы измеряем угловой размер галактики (т. е. угол, который она занимает на небесном своде), знаем ее диаметр, а стало быть, можем вычислить расстояние. Опять триангуляция!
Недавно с помощью гигантского Паломарского телескопа были получены фотографии неимоверно далеких галактик. Одна из этих фотографий приведена на фиг. 5.8. Сейчас полагают, что расстояние до некоторых из них приблизительно равно половине размера Вселенной (1026 м) — наибольшего расстояния, которое можно себе представить!
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

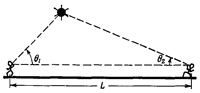 Однако под расстоянием мы понимаем не только то, что можно измерить метром. Как, например, измерить метром расстояние между вершинами двух гор? Здесь на помощь приходит уже другой метод измерения расстояний — триангуляция. Хотя это означает использование другого определения понятия «расстояние», но в тех случаях, когда есть возможность применить оба метода, они дают одинаковый результат. Пространство все же более или менее соответствует представлениям Евклида, поэтому оба определения эквивалентны. Ну, а раз они согласуются на Земле, то мы более уверены в законности применения триангуляции и для больших расстояний. Этим методом была измерена, например, высота первого спутника (фиг. 5.4). Она оказалась равной приблизительно 5*105 м. При большей тщательности измерений тем же самым методом определялось расстояние до Луны. Направления двух телескопов в различных точках Земли дают два необходимых угла. Оказалось, что Луна удалена от нас на расстояние 4*108 м. Однако для Солнца таких измерений провести нельзя, по крайней мере до сих пор никому не удавалось. Дело в том, что точность, с которой можно сфокусировать телескоп на данную точку Солнца и с которой можно измерить углы, не достаточна для вычисления расстояния до Солнца. Как же все-таки определить его? Необходимо как-то расширить принцип триангуляции. Астрономические наблюдения позволяют измерить относительное расстояние между планетами и Солнцем и определить их относительное расположение. Таким образом, мы получаем план солнечной системы в неизвестном масштабе. Чтобы определить масштаб, требуется только абсолютное расстояние, которое было найдено многими различными способами. Один из способов, считавшийся до самого последнего времени наиболее точным, заключается в определении расстояния от Земли до Эроса — малой планеты, которая по временам проходит недалеко от Земли. С помощью триангуляции можно определить расстояние до этого небольшого объекта и получить необходимый масштаб. Зная относительные расстояния, можно определить, например, все абсолютные расстояния от Земли до Солнца или до планеты Плутон.
Однако под расстоянием мы понимаем не только то, что можно измерить метром. Как, например, измерить метром расстояние между вершинами двух гор? Здесь на помощь приходит уже другой метод измерения расстояний — триангуляция. Хотя это означает использование другого определения понятия «расстояние», но в тех случаях, когда есть возможность применить оба метода, они дают одинаковый результат. Пространство все же более или менее соответствует представлениям Евклида, поэтому оба определения эквивалентны. Ну, а раз они согласуются на Земле, то мы более уверены в законности применения триангуляции и для больших расстояний. Этим методом была измерена, например, высота первого спутника (фиг. 5.4). Она оказалась равной приблизительно 5*105 м. При большей тщательности измерений тем же самым методом определялось расстояние до Луны. Направления двух телескопов в различных точках Земли дают два необходимых угла. Оказалось, что Луна удалена от нас на расстояние 4*108 м. Однако для Солнца таких измерений провести нельзя, по крайней мере до сих пор никому не удавалось. Дело в том, что точность, с которой можно сфокусировать телескоп на данную точку Солнца и с которой можно измерить углы, не достаточна для вычисления расстояния до Солнца. Как же все-таки определить его? Необходимо как-то расширить принцип триангуляции. Астрономические наблюдения позволяют измерить относительное расстояние между планетами и Солнцем и определить их относительное расположение. Таким образом, мы получаем план солнечной системы в неизвестном масштабе. Чтобы определить масштаб, требуется только абсолютное расстояние, которое было найдено многими различными способами. Один из способов, считавшийся до самого последнего времени наиболее точным, заключается в определении расстояния от Земли до Эроса — малой планеты, которая по временам проходит недалеко от Земли. С помощью триангуляции можно определить расстояние до этого небольшого объекта и получить необходимый масштаб. Зная относительные расстояния, можно определить, например, все абсолютные расстояния от Земли до Солнца или до планеты Плутон.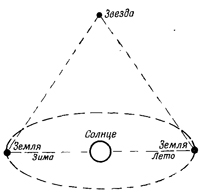 А как измерить расстояние до еще более отдаленных объектов, например до звезд? К счастью, здесь снова можно возвратиться к нашему методу триангуляции, ибо движение Земли вокруг Солнца позволяет измерить расстояние до объектов, находящихся вне солнечной системы. Если мы направим телескоп на некую звезду один раз зимой, а другой раз летом (фиг. 5.5), то можно надеяться достаточно точно измерить углы и определить расстояние до этой звезды.
А как измерить расстояние до еще более отдаленных объектов, например до звезд? К счастью, здесь снова можно возвратиться к нашему методу триангуляции, ибо движение Земли вокруг Солнца позволяет измерить расстояние до объектов, находящихся вне солнечной системы. Если мы направим телескоп на некую звезду один раз зимой, а другой раз летом (фиг. 5.5), то можно надеяться достаточно точно измерить углы и определить расстояние до этой звезды. Но что делать, если звезда находится настолько далеко от нас, что уже невозможно пользоваться методом триангуляции? Астрономы всегда изобретают все новые и новые способы определения расстояний. Так, они научились определять размер и яркость звезд по их цвету. Оказалось, что цвет и истинная яркость многих близлежащих звезд, расстояние до которых определялось методом триангуляции, в большинстве случаев связаны между собой гладкой зависимостью. Если теперь измерить цвет отдаленной звезды, то по этой зависимости можно определить ее истинную яркость, а измеряя видимую яркость звезды (вернее, по тому, насколько звезда нам кажется тусклой), можно вычислить расстояние до нее. (Для данной истинной яркости видимая яркость уменьшается как квадрат расстояния.) Правильность этого метода нашла неожиданное подтверждение в результатах измерений, проведенных для группы звезд, известных под названием «шарового скопления». Фотография этой группы звезд приведена на фиг. 5.6. Достаточно взглянуть на фотографию, чтобы убедиться, что все эти звезды расположены в одном месте. Тот же результат получается и с помощью метода сравнения цвета и яркости.
Но что делать, если звезда находится настолько далеко от нас, что уже невозможно пользоваться методом триангуляции? Астрономы всегда изобретают все новые и новые способы определения расстояний. Так, они научились определять размер и яркость звезд по их цвету. Оказалось, что цвет и истинная яркость многих близлежащих звезд, расстояние до которых определялось методом триангуляции, в большинстве случаев связаны между собой гладкой зависимостью. Если теперь измерить цвет отдаленной звезды, то по этой зависимости можно определить ее истинную яркость, а измеряя видимую яркость звезды (вернее, по тому, насколько звезда нам кажется тусклой), можно вычислить расстояние до нее. (Для данной истинной яркости видимая яркость уменьшается как квадрат расстояния.) Правильность этого метода нашла неожиданное подтверждение в результатах измерений, проведенных для группы звезд, известных под названием «шарового скопления». Фотография этой группы звезд приведена на фиг. 5.6. Достаточно взглянуть на фотографию, чтобы убедиться, что все эти звезды расположены в одном месте. Тот же результат получается и с помощью метода сравнения цвета и яркости.
