Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 50. Гармоники

Качество и гармония

Теперь мы уже можем описать, чем определяется «качество» музыкального тона. Оно определяется относительным количеством различных гармоник, т. е. относительными величинами a и b. Тон, содержащий только первую гармонику, называется «чистым», а тон с несколькими сильными гармониками называется «богатым». Скрипка дает гармоники в одной пропорции, а   гобой — в   другой.
 
Можно «изготовить» различные музыкальные тоны, если подсоединить к громкоговорителю несколько «осцилляторов». (Осциллятор обычно дает приблизительно чистые простые гармонические колебания.) В качестве частот осцилляторов мы выберем ω, 2ω, Зω и т. д. Приделав к каждому осциллятору регулятор громкости, можно смешивать гармоники в любой желаемой пропорции и тем самым создавать звуки различного качества. Примерно так работает электрический орган. Клавиши выбирают частоту основного осциллятора, а педали контролируют относительную пропорцию различных гармоник. С помощью этих регуляторов можно заставить орган звучать как флейту, или как гобой, или как скрипку.
 
Интересно, что для получения такого «искусственного» звука нет никакой необходимости разделять осцилляторы на «синусные»и «косинусные» — для каждой частоты нам достаточно только одного осциллятора. Наше ухо не очень чувствительно к относительной фазе гармоник. Оно воспринимает «синусную» и «косинусную» части частоты в целом. Поэтому наш анализ более точен, чем это необходимо для объяснения субъективной стороны музыки. Однако реакция микрофона или другого физического инструмента все-таки зависит от фазы, и наш полный анализ для таких случаев просто необходим.
 
«Качество» разговорной речи определяется гласными звуками. Форма рта определяет частоты собственных гармоник колебаний звука в нем. Некоторые из этих гармоник возбуждаются звуковыми волнами от голосовых связок. Таким способом происходит усиление одних гармоник по сравнению с другими. Когда мы меняем форму рта, мы даем преимущество гармоникам разных частот над другими. Благодаря этому эффекту, например, имеется разница между звуком «о—о—о» и звуком «а—а—а».
 
Всем известно, что каждый гласный звук, скажем «о—о—о», когда мы говорим или поем, всегда похож сам на себя как при высоких, так и при низких частотах. Из описанного нами механизма мы бы ожидали, что когда мы открываем рот и произносим звук «а—а—а», то тем самым мы выделяем какие-то определенные частоты, которые не должны измениться при повышении голоса. Таким образом, с изменением высоты отношение важных гармоник к основному тону, т. е. то, что мы называем «качеством», должно как будто изменяться. Очевидно, механизм, с помощью которого мы узнаем звуки речи, основан не на соотношении различных гармоник.
 
Что же можно теперь сказать об открытии Пифагора? Мы понимаем, что основные частоты двух струн, длины которых относятся как 2:3, тоже будут относиться как 3:2. Но почему же вместе они «приятно звучат»? Разгадку, по-видимому, нужно искать в частотах гармоник. Вторая гармоника короткой струны будет иметь ту же самую частоту, что и третья гармоника длинной струны. (Легко показать или просто поверить, что, задев струну, мы возбуждаем несколько сильных нижних гармоник.)
 
По-видимому, справедливо следующее правило: ноты звучат гармонично, когда у них есть гармоники с одинаковой частотой. Ноты диссонируют, если их высшие гармоники имеют частоты, близкие друг к другу, но достаточно отличающиеся для того, чтобы между ними возникали быстрые биения. Однако, почему биения звучат неприятно и почему унисон высших гармоник звучит приятно, мы не умеем ни определить, ни описать. Исходя из наших знаний, мы не можем сказать, что должно приятно звучать, так же как, например, что должно приятно пахнуть. Иными словами, наше понимание этого явления не идет дальше простого утверждения, что когда ноты звучат в унисон, то это приятно. Но отсюда, кроме свойства гармонии в музыке, нам ничего не вывести.
 
Гармонические соотношения, которые мы только что описали, легко проверить, проделав несложный опыт на фортепьяно. Давайте обозначим три последовательные ноты до в середине клавиатуры через до, до` и до", а три последовательные ноты соль, расположенные непосредственно выше их, через соль, соль` и соль". Основные гармоники при этом будут иметь следующие относительные частоты:

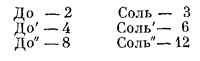Вот как можно продемонстрировать эти гармонические соотношения. Давайте медленно нажмем клавишу до` так, чтобы она не зазвучала, но чтобы демпфер приподнялся. Если теперь нажать до, то вместе с основной гармоникой будет возбуждена и вторая гармоника, которая возбудит основную гармонику струны до`. Если теперь отпустить клавишу до (оставляя нажатой клавишу до`), то демпфер заглушит струну до, и мы можем услышать, как замирает тихий звук струны до`. Точно таким же образом третья гармоника до может вызвать звучание струны соль` или шестая гармоника до (которая звучит гораздо тише) может вызвать колебание основной гармоники струны соль".
 
Совершенно другой результат получится, если мы сначала потихоньку нажмем соль, а затем ударим по клавише до`. Третья гармоника до` будет соответствовать четвертой гармонике соль, так что будет возбуждена только четвертая гармоника соль. Мы можем услышать (если слушать очень внимательно) звук соль", который на две октавы выше, чем соль, которую мы нажали! Можно придумать еще очень много комбинаций этой игры.
 
Попутно заметим, что мажорный лад можно просто определить условием, что каждый из трех мажорных аккордов (фа— ля—до), (до—ми—соль) и (соль—си-бемоль—ре) представляет последовательность тонов с отношением частот (4:5:6). Эти отношения и тот факт, что в октаве (до—до`, соль—соль` и т. д.) частоты относятся как 1 : 2, определяют в «идеальном» случае весь строй, который называется «натуральным, или пифагорий-ским строем». Но обычно клавишные инструменты типа фортепьяно не настраиваются таким образом, а устраивается небольшая «подтасовка», так что для всех возможных начальных тонов отношение частот только приблизительно верно. При таком строе, названном «темперированным», октава (для которой отношение частот по-прежнему равно 1 : 2) делится на 12 равных интервалов, так что отношение частот для каждого интервала равно (2)^1/2. Для квинты отношение частот будет уже не ³/₂, а (2)^7/12 = 1,499, но для большинства людей оно достаточно близко к ³/₂*.
 
Итак, мы установили правила благозвучия через совпадение гармоник. Может быть, это совпадение и является причиной благозвучия? Кто-то утверждал, что два абсолютно чистых тона, т. е. тщательно очищенных от высших гармоник, не дают ощущения благозвучия или неблагозвучия (диссонанса), когда их частоты равны или приблизительно равны ожидаемому отношению. (Это очень сложный эксперимент, поскольку приготовить чистые тоны очень трудно по причинам, которые мы увидим дальше.) Мы не можем с уверенностью сказать, сравнивает ли ухо гармоники или занимается арифметикой, когда мы решаем, что звук нам нравится.

* В основе деления октавы на 12 ступеней лежит открытие Пифагора. Он брал струну, зажимал ее посредине и получал звук на октаву выше, нем звук незажатой струны. Затем половину струны он опять зажимал посредине и получал звук еще на октаву выше и т. д. Точно так же, зажимая последовательно струну на ¹/₃  длины, он каждый раз получал звук выше на квинту. И вот оказалось, что 12 квинт почти точно укладываются на интервале в 7 октав [т. е. 2⁷≈(³/₂)¹²]. Если же теперь от каждой квинты отложить целое число октав вверх и вниз, то каждая первоначальная октава разделится на 12 частей. Так возник пифагорийский строй. Однако беда в том, нто 12 квинт только приблизительно равны 7 октавам, поэтому в разных местах диапазона «лесенки» получались неровные. При развитии мелодии эти неточности накапливались и возникали противные уху интервалы, так называемые «волки», которые страшно досаждали музыкантам. Иногда дело доходило до курьезов. Рассказывают, что известный композитор Жак Рамо сумел так ловко извлекать из органа «волчьи» звуки, что однажды, желая отказаться от должности церковного органиста, привел своей «игрой» в ужас святых отцов и убедил их в своей «бесталанности». Много сил было потрачено на изгнание «волков». Этим, в частности, безуспешно занимались такие умы, как Кеплер и Эйлер. Однако сделать это удалось не физику и не математику, а органисту Андрею Веркмейстеру. Решение его гениально просто: он отказался от чистых квинт, укоротив их как раз настолько, чтобы дюжина вместилась в 7 октав, и несовместимое совместилось, а «волки» исчезли. Так возник современный темперированный   строй.— Прим.   ред.

СМОТРИТЕ ТАКЖЕ: