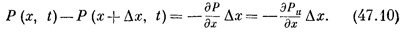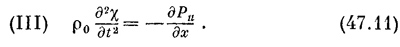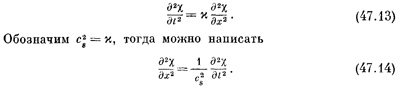| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Волновое уравнение
Итак, физические явления, происходящие в звуковой волне, обладают следующими тремя свойствами:
где давление отнесено к некоторому стандартному давлению Ротн=2*10-10 бар.
можно считать, что изменение давления Рu очень мало по сравнению с Ро, а изменение плотности ρu очень мало по сравнению с ρ0. Тогда
где Ро = f (ρ0) и f(ρ0) — производная от f(ρ), взятая при значении ρ = ρ0. Второе равенство здесь возможно только потому, что ρu очень мало. Таким образом, мы находим, что избыточное давление Рu пропорционально избыточной плотности ρu; коэффициент пропорциональности обозначается через μ:
Это весьма простое соотношение и составляет точное содержание свойства II. Перейдем теперь к свойству I. Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть х, а звук смещает его в момент времени t на величину χ(х, t), так что его новое положение есть x+χ (х, t), как показано на фиг. 47.3. Далее, положение соседнего элемента объема есть х+Δх, и его смещенное положение есть х + Δх + χ (х + Δх, t). Теперь можно найти изменение плотности. Поскольку мы рассматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси х, т. е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале Δх, есть ρ0Δх, где ρ0 —невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, смещенная звуковой волной, будет находиться теперь между x+χ (х, t) и х + Δх + χ (х + Δх, t), причем количество воздуха в этом интервале то же самое, что в интервале Δх до прихода волны. Если через ρ обозначить новую плотность, то
Поскольку Δx мало, можно написать χ(х+Δх, t) — χ(x, t) =(дχ/дх) Δх. Здесь уже появляется частная производная, потому что χ зависит и от ее, и от времени. Наше уравнение принимает вид
Но в звуковой волне все изменения малы, так что ρu мало, χ мало и дχ/дх тоже мало. Поэтому в уравнении, которое мы только что написали,
можно пренебречь ρu(dy/dx) по сравнению с ρ0(dχ/dx). Так мы приходим к соотношению, которое требовалось согласно свойству I:
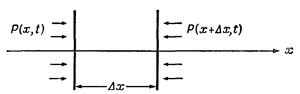
Мы учли, что Δх мало и что только избыточное давление Рu меняется в зависимости от х. Итак, согласно свойству III мы получаем
Теперь уже уравнений достаточно, чтобы увязать все величины и привести к одной переменной, скажем х. Можно выразить Рu в (47.11) с помощью (47.4):
а затем исключить рu с помощью (I). Тогда ρ0 сократится и у нас останется
Это и есть волновое уравнение, которое описывает распространение звука в среде. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

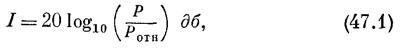
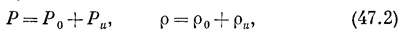
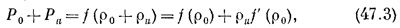
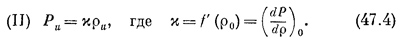
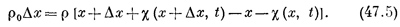
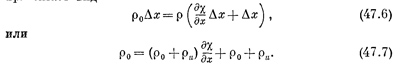
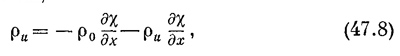

 Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если смещение χ растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.
Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если смещение χ растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.