| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Экспоненциальная атмосфера
Мы уже изучали некоторые свойства большого числа сталкивающихся атомов. Наука, которая занимается этим, называется кинетической теорией, и она описывает свойства вещества, рассматривая, как сталкиваются атомы. Мы утверждаем, что все свойства вещества в целом можно объяснить, рассматривая движение отдельных его частей. Пока мы ограничимся случаем теплового равновесия, т. е. всего лишь подклассом всех явлений природы. Законы механики, применяемые в условиях теплового равновесия, получили название статистической механики, и в этой главе вы немного познакомитесь с некоторыми основными теоремами этой науки. Одна теорема статистической механики вам уже известна. Согласно этой теореме, для любого движения при абсолютной температуре Т средняя кинетическая энергия каждого независимого движения (каждой степени свободы) равна 1/2kT. После этого нам становится кое-что известно о среднем квадрате скорости атомов. Теперь нам необходимо узнать чуть побольше о координатах атомов, чтобы выяснить, много ли их находится при тепловом равновесии в той или иной точке пространства, а также немного подробнее изучить распределение атомов по скоростям. Хотя мы знаем, чему равен средний квадрат скорости, мы все же не можем ответить на вопрос, сколько атомов обладают скоростью, в три раза большей, чем корень из среднего квадрата скорости, или скоростью, равной одной четверти корня из среднего квадрата скорости. А вдруг все атомы имеют одинаковую скорость? Итак, вот два вопроса, на которые мы попытаемся дать ответ: 1) Как атомы располагаются в пространстве, когда на них действуют силы? 2) Каково распределение атомов по скоростям? Заметим, что это два совершенно независимых вопроса и что распределение по скоростям всегда одинаково. Этого можно было ожидать после того, как мы выяснили, что средняя кинетическая энергия степени свободы всегда равна 1/2 kТ, независимо от того, какие силы действуют на молекулы. Распределение по скоростям молекул не зависит от сил, потому что силы не влияют на частоту столкновений. Давайте начнем с примера распределения молекул в атмосфере, подобной той, в которой мы живем, но без ветра или других каких-либо возмущений.
Нам предстоит найти закон, по которому происходит разрежение атмосферы по мере подъема вверх, когда температура на всех высотах одинакова. Если N — полное число молекул в объеме V газа с давлением Р, то PV = NkT, или Р = nkТ, где n — число молекул в единичном объеме. Иначе говоря, если известно число молекул в единичном объеме, то известно и давление, и наоборот: давление и плотность пропорциональны друг другу, ведь температура в нашем случае постоянна. Но давление не может быть постоянным: с уменьшением высоты оно должно возрастать, потому что нижнему слою приходится, так сказать, выдерживать вес всех расположенных сверху атомов. Теперь можно определить, как давление меняется с высотой. Если на высоте h выделить площадку единичной площади, то на эту площадку снизу будет действовать сила, равная давлению Р. Если бы не было силы тяжести, то на площадку на высоте h + dh действовала бы сверху вниз точно такая же сила. Но в нашем случае это не так: действующая снизу сила должна превосходить силу, действующую сверху, на величину, равную весу газа, заключенного между слоями h и h + dh. На каждую молекулу действует сила тяжести mg, где g — ускорение силы тяжести. В интересующем нас слое находится ndh молекул. Это приводит к такому дифференциальному уравнению: Ph+dh— Ph = dP = —mgndh. Поскольку Р = nkТ, а T—постоянная, то можно избавиться или от Р, или от n. Исключим из уравнений Р; тогда получим
Это дифференциальное уравнение говорит нам, как убывает плотность по мере увеличения высоты. Мы располагаем теперь дифференциальным уравнением для плотности частиц n, которая меняется с высотой, но меняется так, что производная плотности пропорциональна себе самой. Функция, производная которой пропорциональна себе самой,— это экспоненциальная функция и, значит, решение дифференциального уравнения имеет вид
Здесь постоянная интегрирования n0— плотность на высоте h = 0 (которую можно задать произвольно); с высотой плотность экспоненциально убывает.
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

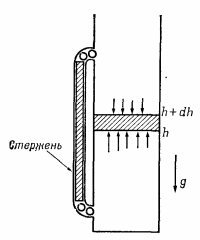 Предположим, что мы имеем дело с довольно высоким столбом газа, находящегося в тепловом равновесии (не так, как в настоящей атмосфере; в ней, как известно, по мере подъема вверх становится холоднее). Укажем здесь, что нарушение равновесия в случае разницы температур на разных высотах можно продемонстрировать, поместив в столб газа металлический стержень так, что его концы соприкасаются с маленькими шариками (фиг. 40.1). Нижние шарики, получая от молекул газа энергию 1/2kТ, передают ее через стержень верхним шарикам и встряхивают их; верхние шарики в свою очередь будут встряхивать соприкасающиеся с ними наверху молекулы. В конце концов, конечно, температура на разных высотах гравитационного поля станет одинаковой.
Предположим, что мы имеем дело с довольно высоким столбом газа, находящегося в тепловом равновесии (не так, как в настоящей атмосфере; в ней, как известно, по мере подъема вверх становится холоднее). Укажем здесь, что нарушение равновесия в случае разницы температур на разных высотах можно продемонстрировать, поместив в столб газа металлический стержень так, что его концы соприкасаются с маленькими шариками (фиг. 40.1). Нижние шарики, получая от молекул газа энергию 1/2kТ, передают ее через стержень верхним шарикам и встряхивают их; верхние шарики в свою очередь будут встряхивать соприкасающиеся с ними наверху молекулы. В конце концов, конечно, температура на разных высотах гравитационного поля станет одинаковой.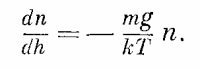

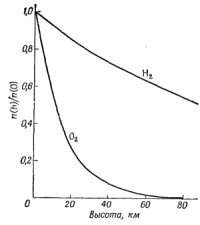 Заметим, что если имеется несколько сортов молекул с разными массами, то число их убывает по разным экспонентам. Число более тяжелых молекул убывает с высотой быстрее, чем число легких молекул. Поэтому можно ожидать, что раз кислород тяжелее азота, то по мере подъема вверх относительное содержание азота в атмосфере (смеси азота и кислорода) будет возрастать. В нашей атмосфере, во всяком случае на доступных высотах, этого фактически не происходит, ибо вследствие воздушных возмущений газы вновь перемешиваются. Ведь это же не изотермическая атмосфера. Тем не менее на больших высотах преобладают очень легкие газы, например водород, так как молекулы легких газов способны забраться на такую высоту, где все остальные экспоненты уже вымрут (фиг. 40.2).
Заметим, что если имеется несколько сортов молекул с разными массами, то число их убывает по разным экспонентам. Число более тяжелых молекул убывает с высотой быстрее, чем число легких молекул. Поэтому можно ожидать, что раз кислород тяжелее азота, то по мере подъема вверх относительное содержание азота в атмосфере (смеси азота и кислорода) будет возрастать. В нашей атмосфере, во всяком случае на доступных высотах, этого фактически не происходит, ибо вследствие воздушных возмущений газы вновь перемешиваются. Ведь это же не изотермическая атмосфера. Тем не менее на больших высотах преобладают очень легкие газы, например водород, так как молекулы легких газов способны забраться на такую высоту, где все остальные экспоненты уже вымрут (фиг. 40.2).