Главная >> Фейнмановские лекции по физике >> Том 3 >> Глава 37. Квантовое поведение Как проследить за электроном?
Попытаемся проделать такой опыт. В наш электронный прибор как раз за стенкой между двумя отверстиями поместим сильный источник света (фиг. 37.4). Известно, что электрические заряды рассеивают свет. Поэтому, каким бы путем электрон ни прошел к детектору, он обязательно рассеет немного света в наш глаз, и мы увидим, где он проскочил. Скажем, если он проскользнет сквозь отверстие 2, как это показано на рисунке, то мы увидим, как где-то около точки А что-то блеснуло. Если же он проскочит сквозь верхнее отверстие, то блеснет где-то поблизости от отверстия 1. А если бы случилось так, что свет блеснет сразу в двух местах, потому что электрон разделился пополам, то ... Но лучше приступим к опыту!
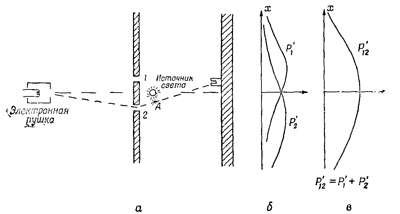 |
Вот что мы увидим: всякий раз, когда мы слышим из детектора «щелк», мы также видим вспышку света или у отверстия 1, или у отверстия 2, но никогда у обоих отверстий сразу! Так происходит при любом положении детектора. Отсюда мы делаем вывод, что когда мы смотрим на электрон, то обнаруживаем, что он проходит или через одно отверстие, или через другое.«Утверждение А», как показывает эксперимент, выполняется с необходимостью.
Что же в таком случае неверно в наших доводах против правильности «Утверждения А»? Почему же все-таки Р12 не равно P1 + Р2? Продолжим наш опыт! Давайте проследим за электронами и посмотрим, что они поделывают. Для каждого полон-гения детектора (для каждого фиксированного х) мы подсчитаем, сколько электронов в него попало, и одновременно проследим (наблюдая вспышки), через какие отверстия они прошли. Следить мы будем так: услышав «щелк», мы поставим палочку в первом столбце, если заметим вспышку у пероого отверстия; если же вспышка блеснет у отверстия 2, то мы отметим это палочкой во второй колонке. Каждый попадающий в детектор электрон будет отнесен к одному из двух классов: либо к классу электронов, проникших сквозь отверстие 1, либо к классу электронов, проникших сквозь отверстие 2. Количество палочек, накопившихся в первой колонке, даст нам Р1` — вероятность того, что электрон пройдет к детектору скяозь-отверстие 1; точно так же вторая колонка даст Р2` — вероятность того, что электрон воспользовался отверстием 2. Повторив эти измерения для многих значений х, мы получим кривые Р1` и Р2`, показанные на фиг. 37.4,б.
Ну что ж, ничего неожиданного в них нет! Кривая P1` вышла похожей на кривую P1, которая получалась, когда отверстие 2 закрывали, а кривая Р2` похожа на то, что мы получали, когда закрывали отверстие 1. Итак, никаких блужданий от дырки к дырке не существует. Когда мы следим за электронами, то оказывается, что они проникают сквозь стенку со щелями в точности так, как мы ожидали. Закрыты ли отверстия или открыты, все равно те электроны, которые мы видели проникающими сквозь отверстие 1, распределены одинаково.
Но погодите! Какова же теперь полная вероятность — вероятность того, что электрон попал в детектор любым путем? У нас уже есть сведения об этом. Сделаем вид, что мы не замечали световых вспышек, т. е. сложим палочки, стоящие в обеих колонках. Нам нужно только сложить числа. Для вероятности того, что электрон попал в поглотитель, пройдя через любое из отверстий, мы действительно получим Р`12 = P1 + Р2. Выходит, что, хоть нам и удалось проследить, через какое отверстие проходят электроны, никакой прежней интерференционной кривой Р12 не вышло, получилась новая кривая Р`12 — кривая без интерференции! А выключите свет — и снова возникнет Р12.
Мы приходим к заключению, что, когда ми смотрим на электроны, распределение их на экране совсем не такое, как тогда, когда на них не смотрят. Уж не от включения ли света меняется ход событий? Должно быть, электроны — вещь очень деликатная; свет, рассеиваясь на электронах, толкает их и меняет их движение. Мы ведь знаем, что электрическое поле, действуя на заряд, прилагает к нему силу. От этого, по-видимому, и следует ожидать изменения движения. Во всяком случае, свет оказывает на электроны большое влияние. Пытаясь «проследить» за электронами, мы изменили их движение. Толчки, испытываемые электронами при рассеянии фотонов, очевидно, таковы, что движение электронов сильно изменяется: электрон, который прежде мог попасть в максимум Р12, теперь приземляется в минимуме P12; вот поэтому никакой интерференции и не заметно.
«Но к чему же такой яркий источник света? — можете вы подумать.— Сбавьте яркость! Световые волны ослабнут и не смогут так сильно возмущать электроны; ослабляя свет все больше и больше, можно в принципе добиться того, что воздействием света на электрон можно будет вообще пренебречь». Будь по-вашему. Давайте попробуем.
Первое, что мы замечаем, это что блеск света, рассеянного на электронах, не слабеет. Сила вспышек остается прежней. От того, что свет стал тускнеть, изменилось лишь одно: временами, услышав щелчок детектора, мы никакой вспышки не замечаем; электрон прошел незамеченным. Мы просто обнаруживаем, что свет ведет себя так же, как электроны: мы знаем, что он «волнист», а теперь убеждаемся, что он к тому же распространяется «порциями». Он доставляется — или рассеивается — порциями, которые мы называем «фотонами». Понижая интенсивность источника света, мы не меняем величины фотонов, а меняем только темп, с каким они испускаются. Этим и объясняется, почему при притушенном свете некоторые электроны проскальзывают к детектору незаметно. Просто как раз в тот момент, когда электрон двигался к детектору, фотона в нужном месте не оказалось.
Все это немного нас обескураживает. Если правильно, что всякий раз, когда мы «видим» электрон, получаются одинаковые вспышки, то все увиденные нами до сего времени электроны были возмущенными электронами. Давайте тогда опыт с тусклым светом проведем иначе. Теперь, услышав щелчок в детекторе, мы будем ставить палочку в одну из трех колонок: в первую, если электрон замечен у отверстия 1, во вторую, если его видели у отверстия 2, и в третью, если его вообще не видели. Обработав данные (рассчитав вероятности), мы получим следующие результаты: «виденные у отверстия 1» будут распределены по закону Р2`, «виденные у отверстия 2» — по закону Р`12 (так что «виденные либо у отверстия 1, либо у отверстия 2» распределяются по закону Рц), а «незамеченные» распределены «волноподобно», как P12 на фиг. 37.3! Если электроны не видимы, возникает интерференция!
Это уже можно понять. Когда мы не видим электрон, значит, фотон не возмутил его; а если уж мы его заметили, значит, он возмущен фотоном. Степень возмущения всегда одна и та же, потому что все фотоны света производят эффекты одинаковой величины, достаточной для того, чтобы смазать любые интерференционные эффекты.
Но нет ли хоть какого-нибудь способа увидеть электрон, не возмущая его? Мы уже говорили о том, что импульс, уносимый фотоном, обратно пропорционален его длине волны (p = h/λ). Чем больше импульс у фотона, тем сильнее он толкает электрон, когда рассеивается на нем. Ага! Раз мы хотим как можно слабее возмущать электроны, то не стоит снижать интенсивность света, лучше снизить его частоту (или, что то же самое, увеличить длину волны). Нужно осветить электроны красным светом. Можно воспользоваться даже инфракрасным светом или радиоволнами (как в радаре). При помощи оборудования, приспособленного для восприятия длинноволнового света, можно тоже разглядеть, куда направился электрон. Может быть, более «мягкий» свет поможет нам избежать сильного возмущения электронов.
Ну что ж, примемся экспериментировать с длинными волнами. Будем повторять наш опыт, увеличивая все больше и больше длину волны. На первых порах ничего не изменится, все результаты будут прежними. А потом произойдет ужасно неприятная вещь. Вы помните, что, изучая микроскоп, мы заметили, что вследствие волновой природы света появляются ограничения на расстояния, на которых два пятна еще не сливаются в одно. Это расстояния порядка длины волны света. И вот теперь это ограничение опять всплывает. Как только длина волны сравняется с промежутком между отверстиями, вспышки станут такими размытыми, что невозможно будет разобрать, возле какого отверстия произошла вспышка! Мы не сможем больше угадывать, какой дыркой воспользовался электрон! Известно, что где-то проскочил, а где — неясно! И это как раз при таком цвете, когда толчки становятся еле заметными, а кривая Р`12 начинает походить на Р12, т. е. начинает чувствоваться интерференция. И только при длинах волн, намного превышающих расстояние между отверстиями (когда уже нет никакой возможности разобрать, куда прошел электрон), возмущение, причиняемое светом, становится таким слабым, что снова появляется кривая Р12 (см. фиг. 37.3).
В нашем опыте мы обнаружили, что невозможно приспособить свет для того, чтобы узнавать, через какое отверстие проник электрон, и в то же время не исказить картины. Гензенберг предположил, что новые законы природы были бы совместимы друг с другом только в том случае, если бы существовали некоторые фундаментальные ограничения на наши экспериментальные возможности, ограничения, которых прежде не замечали. Он предложил в качестве общего принципа свой принцип неопределенности. В терминах нашего эксперимента он звучит следующим образом: «Невозможно соорудить аппарат для определения того, через какое отверстие проходит электрон, не возмущая электрон до такой степени, что интерференционная картина пропадает». Если аппарат способен определять, через ка кую щель проходит электрон, он не способен оказаться столь деликатным, чтобы не исказить картину самым существенным образом. Никому никогда не удалось изобрести или просто указать способ, как обойти принцип неопределенности. Значит, мы обязаны допустить, что он описывает одну из основных характеристик природы.
Полная теория квантовой механики, которой мы в настоящее время пользуемся для описания атомов, а значит, и всего вещества, зависит от правильности принципа неопределенности. Квантовая механика весьма успешно справляется со своими задачами; это укрепляет нашу веру в принцип. Но если когда-нибудь удастся «разгромить» принцип неопределенности, то квантовая механика начнет давать несогласованные результаты и ее придется исключить из рядов правильных теорий явлений природы.
«Ну, хорошо,— скажете вы,— а как же быть с «Утверждением А»? Значит, верно все-таки, что электрон проходит либо сквозь отверстие 1, либо сквозь 2? Или же это неверно?» Единственный ответ, который может быть дан, таков: мы нашли из опыта, что существует некоторый определенный способ, которым мы должны рассуждать, чтобы не прийти к противоречиям.
Вот как мы обязаны рассуждать, чтобы не делать ошибочных предсказаний. Если вы следите за отверстиями, а точнее, если у вас есть прибор, способный узнавать, сквозь какое отверстие из двух проник электрон, то вы можете говорить, что он прошел сквозь отверстие 1 (или 2). Но если вы не пытались узнать, где прошел электрон, если в опыте не было ничего возмущавшего электроны, то вы не смеете думать, что электрон прошел либо сквозь отверстие 1, либо сквозь отверстие 2. Если вы все же начнете так думать и затем делать из этой мысли различные выводы, то, несомненно, натворите ошибок в своем анализе. Вы вынуждены балансировать на этом логическом канате, если хотите успешно описывать природу.
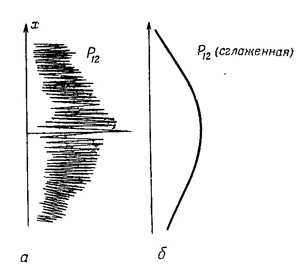 Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть с пулями в нашем первом опыте? Почему мы не увидели там интерференционной картины? Дело оказывается в том, что у пуль длина волны столь незначительна, что интерференционные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдельные максимумы и минимумы. Мы с вами видели только нечто усредненное — это и есть классическая кривая. На фиг. 37.5 мы попытались схематически изобразить, что происходит с крупными телами. На фиг. 37.5, а показано распределение вероятностей для пуль, предсказываемое квантовой механикой. Предполагается, что резкие колебания должны дать представление об интерференционной картине от очень коротких волн. Но любой физический детектор неизбежно вынужден будет накрыть сразу множество зигзагов этой кривой, так что измерения, проведенные с его помощью, дадут плавную кривую, показанную на фиг. 37.5,б. Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть с пулями в нашем первом опыте? Почему мы не увидели там интерференционной картины? Дело оказывается в том, что у пуль длина волны столь незначительна, что интерференционные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдельные максимумы и минимумы. Мы с вами видели только нечто усредненное — это и есть классическая кривая. На фиг. 37.5 мы попытались схематически изобразить, что происходит с крупными телами. На фиг. 37.5, а показано распределение вероятностей для пуль, предсказываемое квантовой механикой. Предполагается, что резкие колебания должны дать представление об интерференционной картине от очень коротких волн. Но любой физический детектор неизбежно вынужден будет накрыть сразу множество зигзагов этой кривой, так что измерения, проведенные с его помощью, дадут плавную кривую, показанную на фиг. 37.5,б.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





 Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть с пулями в нашем первом опыте? Почему мы не увидели там интерференционной картины? Дело оказывается в том, что у пуль длина волны столь незначительна, что интерференционные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдельные максимумы и минимумы. Мы с вами видели только нечто усредненное — это и есть классическая кривая. На фиг. 37.5 мы попытались схематически изобразить, что происходит с крупными телами. На фиг. 37.5, а показано распределение вероятностей для пуль, предсказываемое квантовой механикой. Предполагается, что резкие колебания должны дать представление об интерференционной картине от очень коротких волн. Но любой физический детектор неизбежно вынужден будет накрыть сразу множество зигзагов этой кривой, так что измерения, проведенные с его помощью, дадут плавную кривую, показанную на фиг. 37.5,б.
Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть с пулями в нашем первом опыте? Почему мы не увидели там интерференционной картины? Дело оказывается в том, что у пуль длина волны столь незначительна, что интерференционные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдельные максимумы и минимумы. Мы с вами видели только нечто усредненное — это и есть классическая кривая. На фиг. 37.5 мы попытались схематически изобразить, что происходит с крупными телами. На фиг. 37.5, а показано распределение вероятностей для пуль, предсказываемое квантовой механикой. Предполагается, что резкие колебания должны дать представление об интерференционной картине от очень коротких волн. Но любой физический детектор неизбежно вынужден будет накрыть сразу множество зигзагов этой кривой, так что измерения, проведенные с его помощью, дадут плавную кривую, показанную на фиг. 37.5,б.