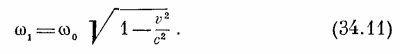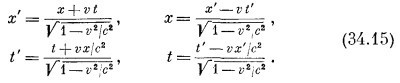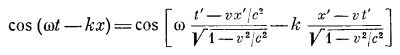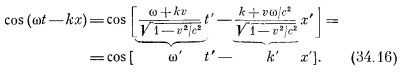| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Эффект Допплера
Можно, конечно, объяснить этот эффект и другими способами. Пусть, например, тот же атом испускает не синусоидальную волну, а короткие импульсы (пип, пип, пип, пип) с некоторой частотой ω1. С какой частотой мы будем их воспринимать? Первый импульс к нам придет спустя определенное время, а второй импульс придет уже через более короткое время, потому что атом за это время успел к нам приблизиться. Следовательно, промежуток времени между сигналами «пип» сократился за счет движения атома. Анализируя эту картину с геометрической точки зрения, мы придем к выводу, что частота импульсов увеличивается в 1/(1—ν/c) раз. Будет ли наблюдаться частота ω = ω0/(1 — ν/c), если атом с собственной частотой ω0 движется со скоростью ν к наблюдателю? Нет. Нам хорошо известно, что собственная частота движущегося атома ω1 и частота покоящегося атома ω0 — не одно и то же из-за релятивистского замедления хода времени. Так что если ω0 — собственная частота покоящегося атома, то частота движущегося атома будет равна
Поэтому наблюдаемая частота ω окончательно равна
Изменение частоты, возникающее в таком случае, называется эффектом Допплера: если излучающий объект движется на нас, излучаемый им свет кажется более синим, а если он движется от нас, свет становится более красным. Приведем еще два других вывода этого интересного и важного результата. Пусть теперь покоящийся источник излучает с частотой ω0, а наблюдатель движется со скоростью ν к источнику. За время t наблюдатель сдвинется на новое расстояние νt от того места, где он был при t = 0. Сколько радиан фазы пройдет перед наблюдателем? Прежде всего, как и мимо любой фиксированной точки, пройдет ω0t, а также некоторая добавка за счет движения источника, а именно νtk0 (это есть число радиан на метр, умноженное на расстояние). Отсюда число радиан за единицу времени, или наблюдаемая частота, равно ω1 = ω0 +k0ν. Весь этот вывод был произведен с точки зрения покоящегося наблюдателя; посмотрим, что увидит движущийся наблюдатель. Здесь мы снова должны учесть разницу в течении времени для наблюдателя в покое и движении, а это значит, что мы должны разделить результат на √1-ν2/c2. Итак, пусть k0 есть волновое число (количество радиан на метр в направлении движения), а ω0 — частота; тогда частота, регистрируемая движущимся наблюдателем, равна
Для света мы знаем, что k0 = ω0/с. Следовательно, в рассматриваемом примере искомое соотношение имеет вид
и, казалось бы, не похоже на (34.12)! Отличается ли частота, наблюдаемая при нашем движении к источнику, от частоты, наблюдаемой при движении источника к нам? Конечно, нет! Теория относительности утверждает, что обе частоты должны быть в точности равны. Если бы мы были достаточно математически подготовлены, то могли бы убедиться, что оба математических выражения в точности равны! В действительности требование равенства обоих выражений часто используется для вывода релятивистского замедления времени, потому что без квадратных корней равенство сразу нарушается. Раз уж мы начали говорить о теории относительности, приведем еще и третий способ доказательства, который покажется, пожалуй, более общим. (Суть дела остается прежней, ибо не играет роли, каким способом получен результат!) В теории относительности имеется связь между положением в пространстве и временем, определяемым одним наблюдателем, и положением и временем, определяемым другим наблюдателем, движущимся относительно первого. Мы уже выписывали эти соотношения (гл. 16). Они представляют собой преобразования Лоренца, прямые и обратные:
Для неподвижного наблюдателя волна имеет вид cos(ωt—kx); все гребни, впадины и нули описываются этой формой. А как будет выглядеть та же самая физическая волна для движущегося наблюдателя? Там, где поле равно нулю, любой наблюдатель при измерении получит нуль; это есть релятивистский инвариант. Следовательно, форма волны не меняется, нужно только написать ее в системе отсчета движущегося наблюдателя:
Произведя перегруппировку членов, получим
Мы снова получим волну в виде косинуса с частотой ω′ в качестве коэффициента при t′ и некоторой другой константой k′ — коэффициентом при х′. Назовем k′ (или число колебаний на 1 м) волновым числом для второго наблюдателя. Таким образом, движущийся наблюдатель отметит другую частоту и другое волновое число, определяемые формулами
Легко видеть, что (34.17) совпадает с формулой (34.13), полученной нами на основании чисто физических рассуждений. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

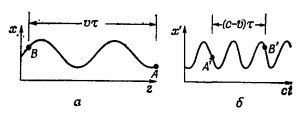 Рассмотрим теперь ряд других эффектов, связанных с движением источника. Пусть источник представляет собой покоящийся атом, колеблющийся со своей обычной частотой ω0. Частота наблюдаемого света тогда будет равна ω0. Но возьмем другой пример: пусть такой же атом колеблется с частотой ω1 и в то же время весь атом, весь осциллятор как целое движется со скоростью ν по направлению к наблюдателю. Тогда истинное движение в пространстве будет таким, как изображено на фиг. 34.10,а. Используем наш обычный прием и добавим сτ, т. е. сместим всю кривую назад и получим колебания, представленные на фиг. 34.10,6. За промежуток времени τ осциллятор проходит расстояние ντ, а на графике с осями х′ и у′ соответствующее расстояние равно (с—ν)τ. Таким образом, число колебаний с частотой ω1 которое укладывалось в интервал Δτ, на новом чертеже укладывается теперь уже в интервал Δτ = (1—ν/с) Δτ; осцилляции сжимаются, и, когда новая кривая будет двигаться мимо нас со скоростью с, мы увидим свет более высокой частоты, увеличенной за счет фактора сокращения (1—ν/c). Итак, наблюдаемая частота равна
Рассмотрим теперь ряд других эффектов, связанных с движением источника. Пусть источник представляет собой покоящийся атом, колеблющийся со своей обычной частотой ω0. Частота наблюдаемого света тогда будет равна ω0. Но возьмем другой пример: пусть такой же атом колеблется с частотой ω1 и в то же время весь атом, весь осциллятор как целое движется со скоростью ν по направлению к наблюдателю. Тогда истинное движение в пространстве будет таким, как изображено на фиг. 34.10,а. Используем наш обычный прием и добавим сτ, т. е. сместим всю кривую назад и получим колебания, представленные на фиг. 34.10,6. За промежуток времени τ осциллятор проходит расстояние ντ, а на графике с осями х′ и у′ соответствующее расстояние равно (с—ν)τ. Таким образом, число колебаний с частотой ω1 которое укладывалось в интервал Δτ, на новом чертеже укладывается теперь уже в интервал Δτ = (1—ν/с) Δτ; осцилляции сжимаются, и, когда новая кривая будет двигаться мимо нас со скоростью с, мы увидим свет более высокой частоты, увеличенной за счет фактора сокращения (1—ν/c). Итак, наблюдаемая частота равна