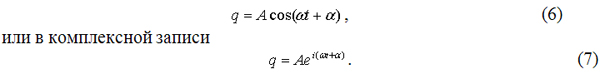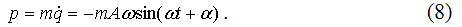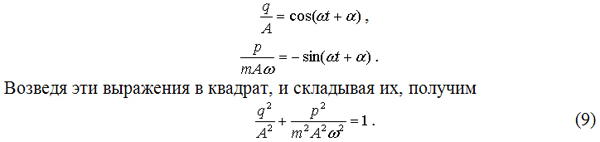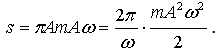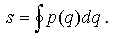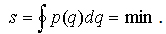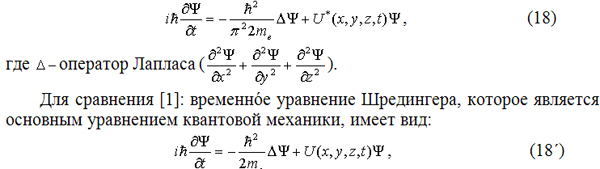Главная >> Разное

Перпетуум мобиле или квантовомеханические системы атомов

В.Л.Андреев
E – mail: [email protected]
“Процесс научных открытий – это, в сущности, непрерывное бегство от чудес”.  
А. Эйнштейн


После того, как в начале XX-го века экспериментально установили, что атом не является элементарной частицей, было предпринято немало попыток создать его физическую модель. Однако дело оказалось столь сложным, что физическая наука была вынуждена отказаться от физической модели, заменив ее моделью математической – очень сложным математическим аппаратом волновой механики, позволяющим получать в физике атома практически полезные результаты.
Предлагаемая мною физическая модель атома – это еще и попытка понять, почему, как только дело касается фундаментальных проблем, физическая наука предпочитает не истину, а ее отражение.     
 
 1. Пусть имеется механическая система, в которой материальная точка (частица) массы m движется со скоростью v из положения a  в положение b, расстояние между которыми по траектории равно l. Осуществленный переход материальной точки назовем событием, к характеристикам которого отнесем: протяжение по пространству l, продление по времени T и действие D, численно равное произведению расстояния l на количество движения материальной точки mv:

или в более общей записи:

Физическая величина  имеет размерность произведения энергия на время, поэтому энергия указанного события  равна:

2. Если в механической системе некоторая совокупность движений материальной точки составляет кругооборот в течение известного промежутка времени T, то такую механическую систему принято называть циклической. К примеру, линейный гармонический осциллятор и планетарная модель атома Бора представляют собой циклические механические системы. Цикл планетарной модели атома водорода составляет одно событие: полный оборот электрона вокруг ядра по орбитальной траектории. Цикл линейного гармонического осциллятора составляют четыре события: два события – движения материальной точки из положения равновесия  в положения крайних отклонений; еще два – возвращение материальной точки в положение равновесия.     
 
3. Предположим, что существует циклическая механическая система, основная особенность которой состоит в том, что все события, происходящие в ней под действием внутрисистемных сил, имеют одинаковую величину действия D, равную значению циклической постоянной Планка ћ:  

Механическую систему, в которой движения материальной  точки удовлетворяют уравнению (3), назовем квантовомеханической.
 
Поскольку в предполагаемой квантовомеханической системе величина действия каждого события неизменна и равна D = ћ > 0, то это означает с необходимостью, что циклы в такой системе повторяются сколь угодно долго, следовательно, предполагаемая квантовомеханическая система представляет собой перпетуум мобиле, т.е. вечно движущееся.
 
Уравнение (3), как видно, выражает принцип устройства перпетуум мобиле, и оно же утверждает, что закономерность этого принципа обусловлена исключительно природой внутрисистемных взаимодействий, поскольку не содержит каких-либо индивидуальных признаков частиц, составляющих квантовомеханическую систему.
 
 4. Из логики уравнения (3) следует, что в квантовомеханических системах природа взаимодействий такова, что действием возникающих в системе сил протяжение любого циклического события по пространству l и импульс материальной точки mv находятся в соотношении:

Следовательно, если в отношении какой-либо механической системы будет достоверно установлено, что она является квантовомеханической, т.е. представляет собой перпетуум мобиле, то из этого факта с необходимостью следует, что вне зависимости от индивидуальных качеств частиц их внутрисистемные взаимодействия отвечают квантовомеханическому закону (4).       
 
5. Мысль о перпетуум мобиле возникает не случайно. Наша Вселенная существует миллиарды лет. Если исходить из того положения, что единство мира состоит в его материальности, то миллиарды лет существуют и атомы, её составляющие. Следовательно, в течение этих же миллиардов лет в атомах движутся электроны, не требуя для своего движения поступления какой либо энергии извне атома. Энергетическая самодостаточность атомов объективно свидетельствует, что в атомах электроны движутся без затраты энергии, следовательно, всякий атом объективно является механической системой перпетуум мобиле. Этим эмпирическим фактом квантовомеханические системы из нашего предположения становятся объективной реальностью: каждый атом, объективно являясь перпетуум мобиле, необходимо является квантовомеханической системой, в которой каждая частица совершает движения в соответствии с уравнением (4). Поэтому, для каждого электрона в атоме справедливо соотношение

а для ядра каждого атома – соотношение

6. Из уравнения движения (5) следует, что при уменьшении скорости электрона до нуля протяжение циклического события по пространству  l возрастает до бесконечности, т.е. при скорости электрона равной нулю уравнение (4), выражающее фундаментальный закон природы, утрачивает рациональный смысл. Но законы природы  рациональны рациональностью бытия, так что если в анализе уравнения, выражающего какой-либо закон природы, появляется иррациональный смысл, то это свидетельствует о формальном подходе к анализу, подходе, не учитывающим действительный физический смысла этого уравнения.
 
Не теряя своей закономерности, уравнение (5) сохраняет рациональный смысл только в том случае, если скорость электрона равная нулю является признаком состоявшегося циклического события. Но тогда этот признак однозначно определяет и физическое содержание самого события: электрон совершил переход по траектории l из положения a, в котором его импульс был равен p=mv, в положение b, в котором его импульс стал равен нулю.  Поскольку атом является системой перпетуум мобиле, то это событие не может быть финитным, а потому уравнение (5) однозначно определяет и полный цикл движения электрона – действием внутрисистемных сил электрон в атоме совершает линейные колебания, с амплитудой равной l.


Следовательно, уравнение (5) является уравнением гармонических колебаний из конечных причин, особенность которого состоит в том, что и  в этом уравнении имеют смысл не текущих значений скорости электрона и пройденного им пути, а значения конечные. Физически это означает, что если полная кинетическая энергия осциллятора равна , то амплитуда его колебаний необходимо находится из уравнения (5).


7. Из логики уравнения (5) следует так же, что в квантовомеханических  системах атома природа взаимодействий такова, что увеличение импульса электрона, вызванное действием тех или иных внешних сил, необходимо приводит к соответствующему “сжатию” траектории l, а уменьшение импульса – к соответствующему её “растяжению”. Из чего следует, что силы, осуществляющие колебания электрона в атоме, электростатическими не являются, поскольку не зависят от положения электрона в поле ядра. Эти силы зависят от скорости движения электрона и величины его массы,  следовательно, порождены они некоторой иной физической реальностью атома, которая квантовомеханическими свойствами взаимодействия с частицами обладает. Поскольку мы не знаем природу этой новой физической реальности, то назовем ее условно пондеромоторным (от лат. pondus, род. п. ponderis – вес, тяжесть и motor – приводящий в движение) полем, а силы, которыми это поле взаимодействует с частицами, назовем пондеромоторными. Именно действием этих сил в атоме осуществляются колебания электрона, следовательно, действием этих сил происходит превращение кинетической энергии электрона в пондеромоторную энергию поля и обратно, что является необходимым условием осуществления колебаний электрона в продлении вечности.
 
При этом следует особо подчеркнуть, что пондеромоторное поле атома не связано непосредственным отношением родства ни с ядром атома, ни с его электронами. Оно существует в атоме, как некая самость, особая форма материальности, прослаивающая потенциальное поле ядра.
 
8. Таким образом, пондеромоторное поле и электрон образуют систему квантового линейного гармонического осциллятора. Поскольку природа действующих сил нам неизвестна, то для описания движений электрона воспользуемся кинематическим уравнением линейного гармонического осциллятора, которое, как известно, безотносительно к действующим силам.
 
Кинематическое уравнение линейного гармонического осциллятора имеет вид

Продифференцировав (6) по времени и умножив полученный результат на массу осциллятора m_e, получим импульс гармонического осциллятора

В каждом положении, характеризуемом отклонением q, осциллятор имеет некоторое значение импульса p. Чтобы найти  p как функцию q, нужно исключить время из уравнений (6) и (8). Для этого представим указанные уравнения в виде:

Координатную плоскость p,q принято называть фазовой плоскостью, а график, показывающий зависимость импульса  p от отклонения q – фазовой траекторией. В соответствии с (9) фазовая траектория гармонического осциллятора представляет собой эллипс, с полуосями  A и mAω. Каждая точка фазовой траектории изображает отклонение  q и импульс p, т.е. состояние осциллятора для некоторого момента времени. С течением времени точка, изображающая состояние перемещается по фазовой траектории против часовой стрелки, совершая за период колебания полный обход. Поэтому колебания линейного гармонического осциллятора можно представить в виде “застывшей” одиночной волны импульса, длина которой равна

Подчеркну, не электрон здесь представляется “застывшей” волной, а колебания электрона представляются волной импульса в фазовой плоскости, что  позволяет более наглядно выразить некоторые соотношения колебательного процесса.
Найдем площадь эллипса. Площадь эллипса S, как известно, равна произведению полуосей эллипса, умноженному на π:

В уравнении колебаний, записанных методом вращающегося вектора амплитуды, выражение mA²ω²₀/2 есть полная энергия осциллятора W, величина  2π/ω равна  1/ν, следовательно, площадь эллипса может быть представлена в виде

Таким образом, энергия гармонического осциллятора пропорциональна площади эллипса S, а коэффициентом пропорциональности является собственная частота осциллятора. Площадь эллипса может быть вычислена так же, как контурный интеграл

В фазовой плоскости площадь эллипса  имеет размерность действия.  Согласно экстремальному принципу Мопертюи, при движении механической системы между двумя ее положениями истинное, т.е. фактически происходящее, ее движение будет отличаться от всех возможных движений тем, что для него значение действия S является наименьшим:   

Но минимальное значение действия S не означает бесконечно малое значение. Приняв, подобно Планку,
S = h
получим выражение полной энергии линейного гармонического осциллятора, который теперь уже является квантовым    

Подставив в уравнение (7) значение A=l, значение ω , найденное из уравнения (11), значение фазы α, найденное применением уравнения (10),

и учитывая, что в квантовой механике показатель экспоненты принято брать со знаком минус, получим  искомое уравнение квантового линейного гармонического осциллятора   

где Ψ идентификатор  системы  квантового осциллятора, в единстве пондеромоторного поля и электрона атома.
9. Рассмотрим влияние электростатического поля ядра на квантовый гармонический осциллятор. Электростатическое поле непосредственно на поле пондеромоторное не действует; его действие опосредовано кулоновскими силами. Кулоновские силы убывают по закону обратных квадратов, следовательно, действие их нелинейно зависит от положения электрона в поле ядра, а потому квантовый осциллятор необходимо становится негармоническим: амплитуда колебаний электрона в направлении ядра становится меньше амплитуды колебаний в направлении противоположном ядру.
Поскольку движения электронов в атоме не доступны непосредственному наблюдению и природа пондеромоторного поля нам неизвестна, то для вывода уравнения негармонического квантового осциллятора воспользуемся уравнением движения электрона из закона сохранения энергии.      
С учетом пондеромоторного поля, полная энергия электрона в электростатическом поле ядра атома равна сумме его кинетической и опосредованной пондеромоторной энергий:

Подставляя в (14) значения энергии  и импульса p² = p²_x + p²_y + p²_z   из (16) и (17) соответственно, получим искомое уравнение негармонического квантового осциллятора 

где, как известно:
– Ψ есть некая волновая функция, в сущности, математическая форма, в отношении которой можно что-то целесообразно мыслить, но которая физически не осуществлена;
– U(x,y,z,t) только потенциальная энергия электрона в поле ядра;
– отсутствие множителя  1/π²обусловлено тем, что при определении фазы α  Шредингер использовал волну де Бройля,  длина которой  λ с одиночной волной импульса λ_p находится в соотношении: λ = λ_pπ/2.    
Однако, несмотря на эти различия, следует признать с необходимостью, что основное уравнение квантовой механики является уравнением квантового осциллятора, и именно этим обстоятельством обусловлена его “магическая” плодотворность в физике атома. Поскольку это уравнение не точное, то при его экспериментальных проверках хорошего совпадения решений уравнения с результатами опыта достигают целесообразными “фантазиями” относительно Ψ-функции и специфических свойств электронов в атоме.  

Перпетуум мобиле или квантовомеханические системы атомов. Часть 2

СМОТРИТЕ ТАКЖЕ: