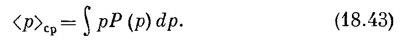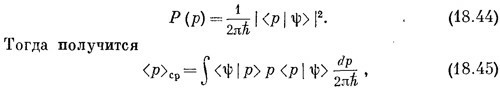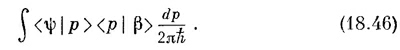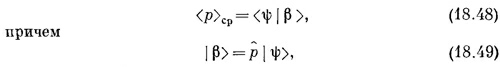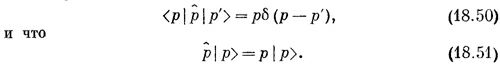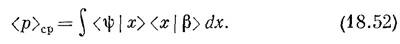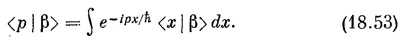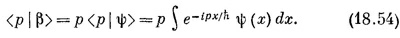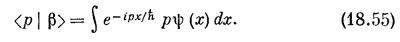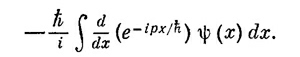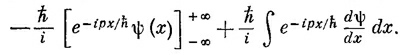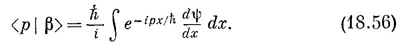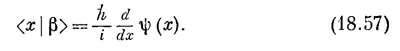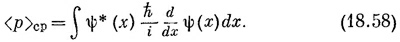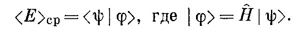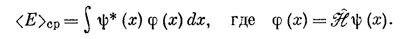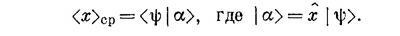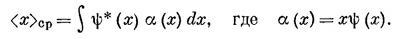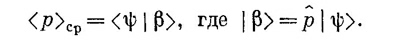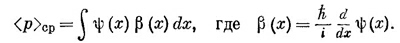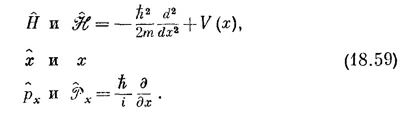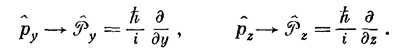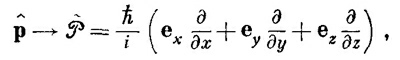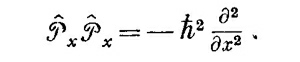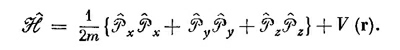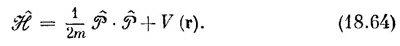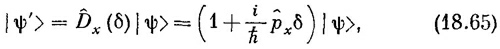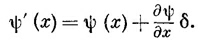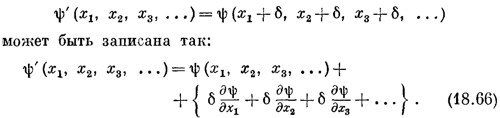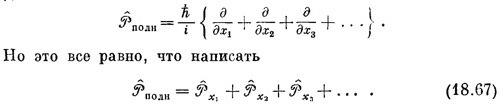| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Оператор импульса
Теперь мы хотим рассчитать средний импульс электрона, опять начав с одномерного случая. Пусть Р(р) dp — вероятность того, что измерение приведет к импульсу в интервале между р и p+dp. Тогда
Обозначим теперь через <р |ψ> амплитуду того, что состояние | ψ> есть состояние с определенным импульсом | р>. Это та же самая амплитуда, которую в гл. 14, § 3, мы обозначали <имп. р | ψ>; она является функцией от р, как <x | ψ> является функцией от х. Затем мы выберем такую нормировку амплитуды, чтобы было
что очень похоже на то, что мы имели для <x>ср.
Теперь вы должны узнать в этом уравнении разложение амплитуды <ψ|β> — разложение по базисным состояниям с определенным импульсом. Из (18.45) следует, что состояние | β> определяется в импульсном представлении уравнением
Иначе говоря, теперь можно писать
где оператор р определяется на языке р-представления уравнением (18.47).
Выводится это так же, как и для х.]
Но теперь надо знать другое: как выглядит состояние |β> в x-представлении. Если мы узнаем это, мы сможем взять интеграл. Итак, наша задача — найти функцию β(x)=<x|β>. Ее можно найти следующим образом. Мы видели в гл. 14, § 3, как <р|β> связано с <x|β>. Согласно уравнению (14.24),
Если нам известно <р|β>, то, решив это уравнение, мы найдем <x|β>. Но результат, конечно, следовало бы как-то выразить через ψ(x)=<x|ψ;>, потому что считается, что именно эта величина нам известна. Будем теперь исходить из (18.47) и, опять применив (14.24), напишем
Интеграл берется по х, поэтому р можно внести под интеграл
Теперь сравним это с (18.53). Может быть, вы подумали, что <x|β> равно pψ(x)? Нет, напрасно! Волновая функция <x|β> = β(x) может зависеть только от х, но не от р. В этом-то вся трудность.
Если это проинтегрировать по частям, оно превратится в
Пока речь идет только о связанных состояниях, ψ (х) стремится к нулю при х→-± ∞, скобка равна нулю и мы имеем
А вот теперь сравним этот результат с (18.53). Вы видите, что
Все необходимое, чтобы взять интеграл в (18.52), у нас уже есть. Окончательный ответ таков:
Мы узнали, как выглядит (18.48) в координатном представлении. Перед нами начинает постепенно вырисовываться интересная картина. Когда мы задали вопрос о средней энергии состояния |ψ>, то ответ был таков:
То же самое в координатном мире записывается так:
Здесь H — алгебраический оператор, который действует на функцию от х.
координатном мире соответствующие уравнения таковы:
Когда мы задали вопрос о среднем значении р, то ответ оказался
В координатном мире эквивалентные уравнения имели бы вид
Во всех наших трех примерах мы исходили из состояния |ψ> и создавали новое (гипотетическое) состояние с помощью квантовомеханичеспого оператора. В координатном представлении мы генерируем соответствующую волновую функцию, действуя на волновую функцию ψ(х) алгебраическим оператором. Можно говорить о взаимнооднозначном соответствии (для одномерных задач) между
В этом перечне мы ввели новый символ Ρх для алгебраического оператора (h/i)∂/∂x:
и поставили под P значок х, чтобы напомнить, что имеем пока дело с одной только x-компонентой импульса.
При желании можно даже говорить об операторе вектора импульса и писать
где ех, еy и еz — единичные векторы в трех направлениях. Можно записать это и еще изящнее:
Окончательный вывод наш таков: по крайней мере для некоторых квантовомеханических операторов существуют соответствующие им алгебраические операторы в координатном представлении. Все, что мы до сих пор вывели (с учетом трехмерности мира), подытожено в табл. 18.1. Каждый оператор может быть представлен в двух равноценных видах :
либо
Теперь мы дадим несколько иллюстраций применения этих идей. Для начала выявим связь между P и H. Если применить Px дважды, получим
Это означает, что можно написать равенство
Или, в векторных обозначениях,
(Члены в алгебраическом операторе, над которыми нет символа оператора ˆ, означают простое умножение.) Это уравнение очень приятно, потому что его легко запомнить, если вы еще не забыли курса классической физики. Хорошо известно, что энергия (нерелятивистская) состоит из кинетической энергии р2/2т плюс потенциальная, а у нас H — тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь сильное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безразличен.
В гл. 15 мы определили оператор рх через оператор смещения Dx [см. формулу (15.27)]:
где δ — малое смещение. Мы должны показать, что это эквивалентно нашему новому определению. В соответствии с тем, что мы только что доказали, это уравнение должно означать то же самое, что и
Но в правой части стоит просто разложение ψ(x + δ) в ряд Тэйлора, а ψ(x + δ)— то, что получится, если сместить состояние влево на δ (или сдвинуть на столько же вправо систему координат). Оба наши определения р согласуются!
Согласно уравнению (18.65), оператор импульса состояния |ψ > (назовем его полным импульсом) равняется
Операторы импульса подчиняются тому правилу, что полный импульс есть сумма импульсов отдельных частей. Здесь, как видите, все чудесным образом переплетено и разные вещи взаимно согласуются. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.