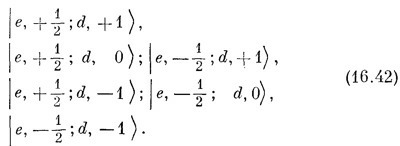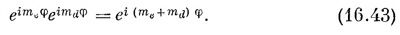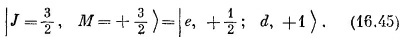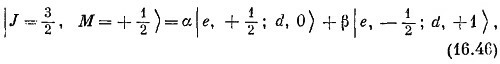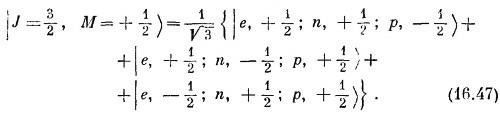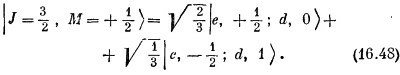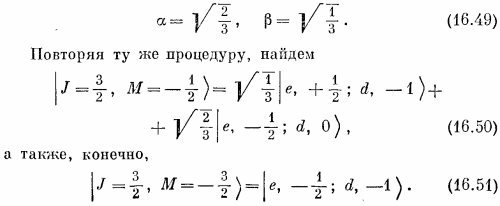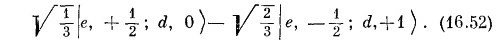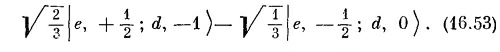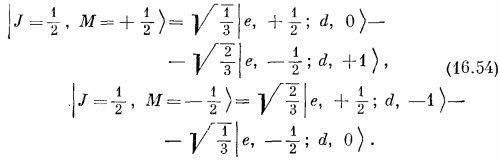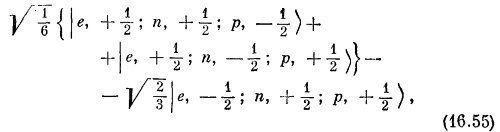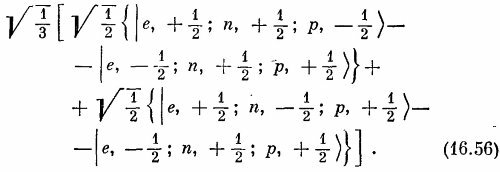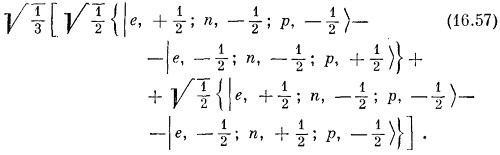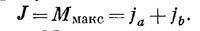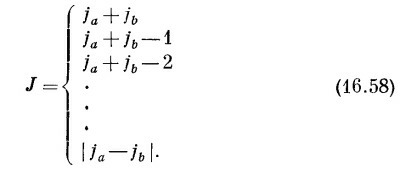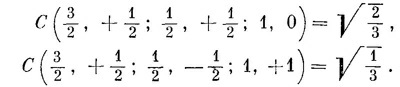| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Сложение моментов количества движения
Когда мы изучали сверхтонкую структуру атома водорода в гл. 10 (вып. 8), нам пришлось рассчитывать внутренние состояния системы, составленной из двух частиц — электрона и протона — со спинами 1/2. Мы нашли, что четверка возможных спиновых состояний такой системы может быть разбита на две группы — на тройку состояний с одной энергией, которая во внешнем поле выглядела как частица со спином 1, и на одно оставшееся состояние, которое вело себя как частица со спином 0. Иначе говоря, объединяя две частицы со спином 1/2, можно образовать систему, «полный спин» которой равен либо единице, либо нулю. В этом параграфе мы хотим рассмотреть на более общем уровне спиновые состояния системы, составленной из двух частиц с произвольными спинами. Это другая важная проблема, связанная с моментами количества движения кванто-вомеханической системы.
Правый столбец показывает, как составляются эти состояния из значений т двух частиц а и b.
Обратите внимание, что мы разверстали состояния согласно значениям суммы те и md в порядке ее убывания.
(Состояние можно считать произведением | е, те> | d, md>, и каждый вектор состояния независимо привнесет свой собственный экспоненциальный множитель.) Множитель (16.43) имеет форму е¡Mφ, поэтому z-компонента момента количества движения у состояния | е, те; d, md> окажется равной
Иначе говоря, z-компонента полного момента количества движения есть сумма z-компонент моментов количества движения отдельных частей.
Но что является состоянием |J = 3/2, М = + 1/2 >? Кандидатов здесь два, они стоят во второй строчке (16.42), и всякая их ли нейная комбинация тоже даст М = + 1/2. Значит, в общем случае можно ожидать, что
где α и β — два числа. Их именуют коэффициенты Клебша — Гордона. Найти их и будет нашей очередной задачей.
То, что стоит в правой части, можно, очевидно, составить из двух членов во второй строчке табл. 16.4, взяв √2/3 от первого члена и √1/3 от второго. Иначе говоря, (16.47) эквивалентно
Мы нашли два наших первых коэффициента Клебша — Гордона α и β [см. (16.46)]:
Это и есть правила составления из спина 1 и спина 1/2 полного спина J = 3/2. Мы свели (16.45) и (16.50) в табл. 16.5.
Но у нас пока есть только четыре состояния, а у системы, которую мы рассматриваем, их шесть.
Точно так же из двух состояний в третьей строке (16.42) можно скомбинировать два взаимно-ортогональных состояния, каждое с М=— 1/2. То, которое ортогонально к (16.50), имеет вид
Это и есть два оставшихся состояния. У них М = me+md±1/2; эти состояния должны соответствовать J = 1/2. Итак, мы имеем
Можно убедиться, что эти два состояния действительно ведут себя как состояния объекта со спином 1/2; для этого надо выразить дейтронную часть через нейтронные и протонные состояния (при помощи табл. 16.3). Первое состояние в (16.53) превратится в
а это можно переписать так:
Посмотрите теперь на выражение в первых фигурных скобках и подумайте, что получается при объединении е и р. Вместе они образуют состояние с нулевым спином (см. нижнюю строку в табл. 16.3) и не дают вклада в момент количества движения. Остался только нейтрон, значит, вся первая фигурная скобка (16.56) будет вести себя при поворотах как нейтрон, а именно как состояние с J= 1/2 , М=±1/2.
Вы легко проверите, что это совпадает со второй строчкой в (16.54), как и полагается, если каждая скобка представляет собой одно из двух состояний системы со спином 1/2. Значит, наши результаты подтвердились. Дейтрон и электрон могут существовать в шести спиновых состояниях, четыре из которых ведут себя как состояния объекта со спином 3/2 (табл. 16.5), а два — как объект со спином 1/2 (16.54).
Поставим теперь себе общую задачу найти состояния, которые можно образовать, объединяя два объекта с произвольными спинами. Скажем, у одного спин ja (так что его z-компонента та пробегает 2jа+1 значений от — ja до +ja), а у другого jb (с z-компонентой тb, пробегающей значения от — jb до +jb).
Следующему значению М, меньшему чем Ммакс на единицу, будут соответствовать два состояния (либо та, либо ть меньше своих максимальных значений на единицу). Из них должно быть образовано одно состояние, принадлежащее совокупности с J=ja+jb , и останется еще одно, которое будет принадлежать новой совокупности с J=ia+jb — 1. Следующее значение М (третье сверху) можно составить тремя путями (из ma=ja — 2, mb=jb, из ma=ja — 1, mb=jb — 1 и из ma = ja, mb=jb — 2). Два из них принадлежат к уже начавшим составляться группам; третье говорит нам, что надо включить в рассмотрение и состояния с J=ja+jb — 2. Такие рассуждения будут продолжаться до тех пор, пока уже нельзя будет, меняя то одно, то другое т, получать новые состояния.
(Написав | ja — jb | вместо jа — jь, мы можем избежать напоминания о том, что ja≥jb.)
Мы не будем здесь подсчитывать коэффициенты для других частных случаев. Но вы обнаружите такие таблицы во многих книжках. Попробуйте сами подсчитать другой случай, например объединение двух объектов со спином 1. Мы же просто привели в табл. 16.7 окончательный результат.
Эти законы объединения моментов количества движения имеют очень важное значение в физике частиц, их приложениям поистине нет конца. К сожалению, у нас нет сейчас больше времени на другие примеры. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.