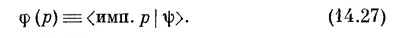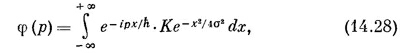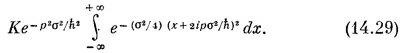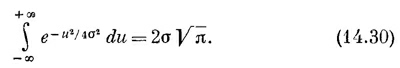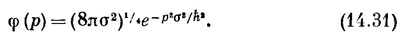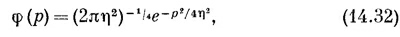| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Состояния с определенным импульсом
Пусть у нас имеется электрон в состоянии | ψ>, описываемом амплитудой вероятности <x | ψ> = ψ (х). Мы знаем, что ψ (х) обозначает состояние, в котором электрон размазан по прямой по какому-то закону, так что вероятность обнаружить его в узком интервале dx близ точки х попросту равна
Что можно сказать об импульсе этого электрона? Можно спросить, какова вероятность того, что импульс этого электрона равен р? Начнем с расчета амплитуды того, что состояние | ψ> присутствует в другом состоянии | имп. р>, которое мы определим как состояние с определенным импульсом р. Эту амплитуду можно найти, применяя наше основное уравнение для разложения амплитуд (14.20). В терминах состояний | имп. р>
А вероятность того, что у электрона будет обнаружен импульс р, выразится квадратом абсолютной величины этой амплитуды. Но опять возникает тот же вопрос насчет нормирования. Ведь вообще можно говорить только о вероятности обнаружить электрон с импульсом в узкой области dp близ значения р. Вероятность того, что импульс в точности равен р, равна нулю (разве что состояние | ψ> окажется состоянием с определенным импульсом). Только вероятность обнаружить импульс в интервале dp возле значения р может оказаться конечной. Нормировку можно делать по-разному. Мы выберем тот способ нормировки, который нам кажется особенно удобным, хотя вам сейчас это может так и не показаться.
Это определение дает нам нормировку амплитуды (имп. р \ ху. Амплитуда <имп. р | х>, естественно, комплексно сопряжена с амплитудой <х | имп. p>, а последнюю мы писали в (14.15). При нашей нормировке оказывается, что коэффициент пропорциональности перед экспонентой как раз равен единице, т. е.
Тогда (14.21) превращается в
Вместе с (14.22) это уравнение позволяет находить распределение импульсов для любого состояния |ψ>.
Распределение вероятности иметь то или иное значение х для такой волновой функции дается ее квадратом
Подстановка (14.25) в (14.24) дает
также переписать в форме
Сделаем теперь замену и = х + 2ipσ2/h; интеграл обратится в
Математикам, вероятно, не понравился бы такой путь расчета, однако итог, несмотря на это, верен:
Мы пришли к интересному результату — распределение амплитуд по р имеет в точности ту же математическую форму, как и распределение амплитуд по х, только ширина кривой Гаусса иная. Можно записать это так:
где полуширина η распределения по р связана с полушириной σ распределения по х формулой
Наш результат утверждает: если сделать распределение по х очень узким, взяв σ малым, то η станет большим и распределение по р сильно расползется. Или наоборот, если распределение по р узко, то оно соответствует широкому распределению по х. Мы можем, если угодно, рассматривать η и σ как некую меру неопределенности локализации импульса и координаты электрона в изучаемом нами состоянии. Если обозначить их соответственно Δр и Δх, то (14.33) обратится в
Интересно вот что: можно доказать, что при всяком ином виде распределения по х или по р произведение ΔрΔх не может стать меньше, чем у нас получилось. Гауссово распределение дает наименьшее возможное значение произведения средних квадратичных. В общем случае
Это количественная формулировка принципа неопределенности Гейзенберга, который качественно нам уже давно известен. Мы обычно делали приближенное утверждение: наименьшее значение произведения ΔрΔх — это число порядка h. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

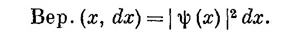
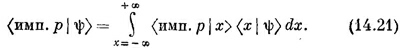
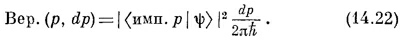
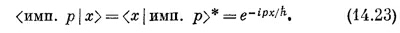
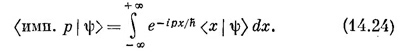

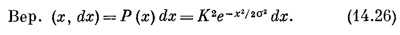
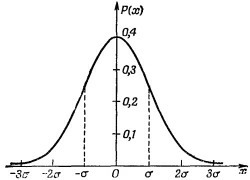 Функция плотности вероятности Р (х) — это кривая Гаусса, показанная на фиг. 14.1. Большая часть вероятности сосредоточена между х = +σ и х = — σ. Мы говорим, что «полуширина» кривой есть σ. (Точнее, σ равняется средней квадратичной координате х, если разброс координат соответствует этому распределению.) Коэффициент К следовало бы выбрать так, чтобы плотность вероятности Р (х) не просто была пропорциональна вероятности (на единицу длины х) обнаружить электрон, но имела бы такой масштаб, чтобы Р (х) Δх равнялось вероятности обнаружить электрон в Δх вблизи х. Коэффициент К, при котором так и получается, можно найти из требования –∞∫+∞Р (х) dx = 1, потому что вероятность, обнаружить электрон где попало равна единице. Мы находим, что К = (2πσ2)–1/4.
Функция плотности вероятности Р (х) — это кривая Гаусса, показанная на фиг. 14.1. Большая часть вероятности сосредоточена между х = +σ и х = — σ. Мы говорим, что «полуширина» кривой есть σ. (Точнее, σ равняется средней квадратичной координате х, если разброс координат соответствует этому распределению.) Коэффициент К следовало бы выбрать так, чтобы плотность вероятности Р (х) не просто была пропорциональна вероятности (на единицу длины х) обнаружить электрон, но имела бы такой масштаб, чтобы Р (х) Δх равнялось вероятности обнаружить электрон в Δх вблизи х. Коэффициент К, при котором так и получается, можно найти из требования –∞∫+∞Р (х) dx = 1, потому что вероятность, обнаружить электрон где попало равна единице. Мы находим, что К = (2πσ2)–1/4.