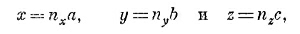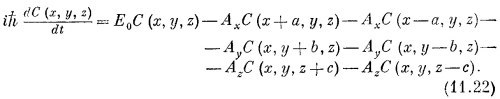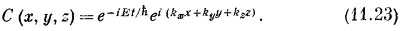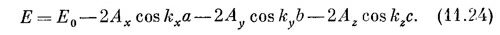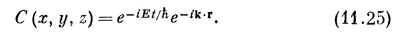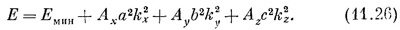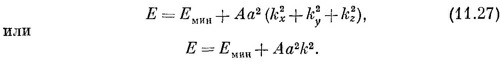Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 11. Распространение в кристаллической решетке

Электрон в трехмерной решетке

Еще немного о том, как можно применить те же идеи, чтобы понять, что происходит с электроном в трех измерениях. Результаты оказываются очень похожими. Пусть имеется прямоугольная решетка атомов с расстояниями а, b, c в трех направлениях. (Если вам больше по душе кубическая решетка, примите все расстояния равными друг другу.) Предположим также, что амплитуда прыжка к соседу в направлении х есть ¡А _х/h; амплитуда прыжка в направлении у есть iA_y/h, а амплитуда прыжка в направлении z есть iA_z/h. Как же описать базисные состояния? Как и в одномерном случае, одно базисное состояние — это когда электрон находится близ атома с координатами х, у, z, где (х, у, z) — одна из точек решетки. Если выбрать начало координат в одном из атомов, то все зти точки придутся на

где n_х, n_y , n_z —три целых числа. Вместо того чтобы ставить при х, у и z их номера, будем просто писать х, у, z, имея в виду, что они принимают лишь такие значения, которые бывают у точек решетки. Итак, базисное состояние изображается символом |электрон в х, у, z>, а амплитуда того, что электрон в некотором состоянии | ψ> окажется в этом базисном состоянии, есть С (х, у, z) = < электрон в х, у, z |ψ>.
 
Как и прежде, амплитуды С (х, у, z) могут меняться во времени. При наших предположениях гамильтоновы уравнения обязаны выглядеть следующим образом:

Хоть это и выглядит громоздко, но вы сразу, конечно, пеймете, откуда взялось каждое слагаемое.
 
Опять попробуем найти стационарное состояние, в котором все С меняются со временем одинаково. И снова решение есть экспонента

Если вы подставите это в (11.22), то увидите, что оно вполне подойдет, если только энергия Е будет связана с k_х, k_у и k_z следующим образом:

Теперь энергия зависит от трех волновых чисел   k_х, k_y ,k_z, которые, кстати, есть компоненты трехмерного вектора k. И действительно, (11.23) можно переписать в векторных обозначениях:

Амплитуда меняется как комплексная плоская волна, которая движется в трехмерном пространстве в направлении k с волновым числом k = (k_x² + к_y² + к_z²)^1/2.
 
Энергия, связываемая с этими стационарными состояниями, зависит от трех компонент к сложным образом, подчиняясь уравнению (11.24). Характер изменения Е зависит от относительных знаков и величин А_х, А_y и A_z. Если вся эта тройка положительна и если нас интересуют лишь маленькие k, то зависимость оказывается сравнительно простой.
 
Разлагая косинус, как и раньше [см. (11.16)], мы теперь придем к

В простой кубической решетке с расстоянием а между узлами следует ожидать, что и А_х, и А_y , и A_z будут все равны друг другу (скажем, равны А), так что получилось бы

А это как раз совпадает с (11.16). Повторяя те же рассуждения, что и тогда, мы пришли бы к заключению, что электронный пакет в трех измерениях (составленный путем суперпозиции множества состояний с почти одинаковыми энергиями) также движется на манер классической частицы, обладающей некоторой эффективной массой.
 
В кристалле не с кубической, а с более низкой симметрией (или даже в кубическом кристалле, но таком, в котором состояние электрона около атома несимметрично) три коэффициента А _х, А_у и А_z различны. Тогда «эффективная масса» электрона, сосредоточенного в узкой области, зависит от направления его движения. Может, например, оказаться, что у него разная инерция при движении в направлении х и при движении в направлении у. (Детали такого положения вещей иногда описываются с помощью «тензора эффективной массы».)

СМОТРИТЕ ТАКЖЕ: