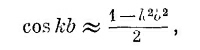Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 11. Распространение в кристаллической решетке Состояния определенной энергии
Об электроне в решетке мы теперь уже можем узнать очень многое. Для начала попробуем отыскать состояния определенной энергии. Как мы видели в предыдущих главах, это означает, что надо отыскать такой случай, когда все амплитуды меняются с одной частотой, если только они вообще меняются. Мы ищем решение в виде
Комплексное число аn говорит нам о том, какова не зависящая от времени часть амплитуды того, что электроны будут обнаружены возле n-го атома. Если это пробное решение подставить для проверки в уравнения (11.4), то получим
Перед нами бесконечное число уравнений для бесконечного количества неизвестных аn ! Ситуация тяжелая!
Но мы знаем, что надо только взять детерминант... нет, погодите! Детерминанты хороши, когда уравнений два, три или четыре. Но здесь их очень много, даже бесконечно много, и вряд ли от детерминантов будет толк. Нет, лучше попробовать решать эти уравнения прямо. Во-первых, пронумеруем положения атомов; будем считать, что n-й атом находится в хn, а (n+1)-й— в хn + 1. Если расстояние между атомами равно b (как на фиг. 11.1), то хn + 1 = хn+b. Взяв начало координат в атоме номер нуль, можно даже получить хn = nb. Уравнение (11.5) можно тогда переписать в виде
а уравнение (11.6) превратится в
Пользуясь тем, что хn+1 = хn+b, это выражение можно также записать в виде
Это уравнение немного походит на дифференциальное. Оно говорит, что величина а(х) в точке хn связана с той же физической величиной в соседних точках хn ± b. (Дифференциальное уравнение связывает значения функции в точке с ее значениями в бесконечно близких точках.) Может быть, здесь подойдут методы, которыми мы обычно пользуемся для решения дифференциальных уравнений? Попробуем.
Решения линейных дифференциальных уравнений с постоянными коэффициентами всегда могут быть выражены через экспоненты. Попробуем и здесь то же самое; в качестве пробного решения выберем
Тогда (11.9) обратится в
Сократим на общий множитель е¡kxn; получим
Два последних члена равняются 2А cos kb, так что
Мы обнаружили, что при любом выборе постоянной k имеется решение, энергия которого дается этим уравнением. В зависимости от k получаются различные возможные энергии, и каждая k соответствует отдельному решению. Решений бесконечно много, но это и не удивительно, ведь мы исходим из бесконечного числа базисных состояний.
Посмотрим, каков смысл этих решений. Для каждой k уравнение (11.10) дает свои а. Тогда амплитуды обращаются в
 |
 причем нужно помнить, что энергия Е также зависит от А; в согласии с уравнением (11.13). Множитель eikxn дает пространственную зависимость амплитуд. Амплитуды при переходе от атома к атому колеблются. причем нужно помнить, что энергия Е также зависит от А; в согласии с уравнением (11.13). Множитель eikxn дает пространственную зависимость амплитуд. Амплитуды при переходе от атома к атому колеблются.
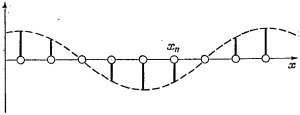
При этом имейте в виду, что колебания амплитуды в пространстве комплексны, модуль ее вблизи любого атома один и тот же, а фаза (в данный момент) от атома к атому сдвигается на ikb. Чтобы можно было видеть, что происходит, поставим у каждого атома вертикальную черточку, равную вещественной части амплитуды (фиг. 11.2). Огибающая этих вертикалей (показанная штрихованной линией) является, конечно, косинусоидой. Мнимая часть Сn — это тоже колеблющаяся функция, но она сдвинута по фазе на 90°, так что квадрат модуля (сумма квадратов вещественной и мнимой частей) у всех С один и тот же.
Итак, выбирая k, мы получаем стационарное состояние с определенной энергией Е. И в каждом таком состоянии электрону одинаково вероятно оказаться около любого из атомов, никаких преимуществ у одного атома перед другим нет. От атома к атому меняется только фаза. Фазы меняются еще и со временем. Из (11.14) следует, что вещественная и мнимая части распространяются по кристаллу, как волны, как вещественная и мнимая части выражения
 |
 Волна может двигаться либо к положительным, либо к отрицательным х, смотря по тому, какой знак выбран для k. Волна может двигаться либо к положительным, либо к отрицательным х, смотря по тому, какой знак выбран для k.
Заметьте, что мы предположили, что поставленное в нашем пробном решении (11.10) число k есть число вещественное. Теперь видно, почему в бесконечной цепочке атомов так и должно быть. Пусть k было бы мнимым числом —ik′. Тогда амплитуды аn менялись бы, как еk′хn, что означало бы, что амплитуда растет все выше и выше, когда х возрастает, или при k′ отрицательном, когда х становится большим отрицательным числом. Такой вид решения был бы вполне хорош, если бы цепочка атомов на чем-то кончалась, но в бесконечной цепи атомов это не может быть физическим решением. Оно привело бы к бесконечным амплитудам и, стало быть, к бесконечным вероятностям, которые не могут отражать действительного положения вещей. Позже мы встретимся с примером, когда и у мнимых k есть смысл.
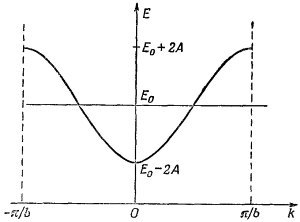
Соотношение (11.13) между энергией Е и волновым числом k изображено на фиг. 11.3. Как следует из этого рисунка, энергия может меняться от Е0–2А при k = 0 до Е0 + 2А при k=±π/b. График начерчен для положительных А, при отрицательных А кривую пришлось бы перевернуть, но область изменения осталась бы прежней. Существенно то, что в некоторой области, или «полосе» энергий допустимы любые значения энергии; вне полосы энергии быть не может. Из наших предположения следует, что если электрон в кристалле находится в стационарном состоянии, энергия его не сможет оказаться вне этой полосы.
Согласно (11.10), меньшие k отвечают более низким энергетическим состояниям Е≈Е0—2А. Когда k по величине растет (все равно, в положительную или отрицательную сторону), то энергия сперва растет, а потом при k = ±π/b достигает максимума, как показано на фиг. 11.3. Для k, больших, чем π/b, энергия опять начала бы убывать. Но такие k рассматривать не стоит, они не приведут к каким-либо новым состояниям, а просто повторяют те состояния, которые уже появлялись при меньших k. Вот как в этом можно убедиться. Рассмотрим состояние наинизшей энергии, для которого k = 0. Тогда при всех хn коэффициент а (хn) будет один и тот же [см. (11.10)]. Та же самая энергия получилась бы и при k = 2π/b. Тогда из (11.10) следовало бы
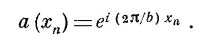 |
Но, считая, что начало координат приходится на х0, можно положить хn = nb, и тогда а (хn) превратится в
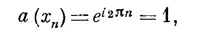 |
 т. е. состояние, описываемое этими а (хn), физически ничем не будет отличаться от состояний при k = 0. Оно не представляет особого решения. т. е. состояние, описываемое этими а (хn), физически ничем не будет отличаться от состояний при k = 0. Оно не представляет особого решения.
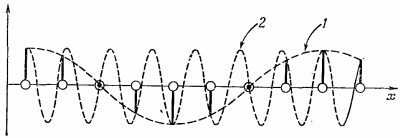
В качестве другого примера возьмем k = π/4b. Вещественная часть а (хn) изображена на фиг. 11.4 кривой 1. Если бы k было в семь раз больше (k=7π/4b), то вещественная часть а (хn) менялась бы так, как показано на кривой 2. (Сама косинусоида смысла не имеет, важны только ее значения в точках хn. Кривые нужны просто для того, чтобы было видно, как все меняется.) Вы видите, что оба значения k во всех хn дают одинаковые амплитуды.
Вывод из всего этого состоит в том, что все возможные решения нашей задачи получатся, если взять k только из некоторой ограниченной области. Мы выберем область от —π/b до +π/b (она показана на фиг. 11.3). В этой области энергия стационарных состояний с ростом абсолютной величины k возрастает.
Еще одно побочное замечание о том, с чем было бы забавно повозиться. Представьте, что электрон может не только перепрыгивать к ближайшим соседям с амплитудой iA/h, но имеет еще возможность одним махом перепрыгивать и к следующим за ними соседям с некоторой другой амплитудой iB/h. Вы опять обнаружите, что решение можно искать в форме аn = е¡kxn, этот тип решений является универсальным. Вы также увидите, что стационарные состояния с волновым числом k имеют энергию Е0—2А cos kb—2В cos 2kb. Это означает, что форма кривой Е как функции k не универсальна, а зависит от тех частных допущений, при которых решается задача. Это не обязательно косинусоида, и она даже не обязательно симметрична относительно горизонтальной оси. Но зато всегда верно, что кривая вне интервала (—π/b, π/b) повторяется, так что заботиться о других значениях k не нужно.
Посмотрим еще внимательнее на то, что происходит при малых k, когда вариации амплитуд между одним хn и соседним очень маленькие. Будем отсчитывать энергию от такого уровня, чтобы было Е0 = 2A; тогда минимум кривой фиг. 11.3 придется на нуль энергии. Для достаточно малых k можно написать
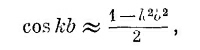 |
и энергия (11.13) превратится в
Получается, что энергия состояния пропорциональна квадрату волнового числа, описывающего пространственные вариации амплитуд Сn.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





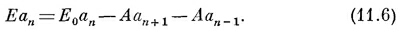

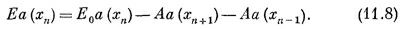
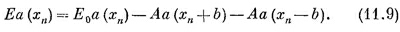

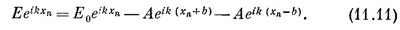
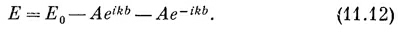
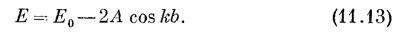

 причем нужно помнить, что энергия Е также зависит от А; в согласии с уравнением (11.13). Множитель eikxn дает пространственную зависимость амплитуд. Амплитуды при переходе от атома к атому колеблются.
причем нужно помнить, что энергия Е также зависит от А; в согласии с уравнением (11.13). Множитель eikxn дает пространственную зависимость амплитуд. Амплитуды при переходе от атома к атому колеблются.
 Волна может двигаться либо к положительным, либо к отрицательным х, смотря по тому, какой знак выбран для k.
Волна может двигаться либо к положительным, либо к отрицательным х, смотря по тому, какой знак выбран для k.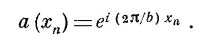
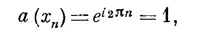
 т. е. состояние, описываемое этими а (хn), физически ничем не будет отличаться от состояний при k = 0. Оно не представляет особого решения.
т. е. состояние, описываемое этими а (хn), физически ничем не будет отличаться от состояний при k = 0. Оно не представляет особого решения.