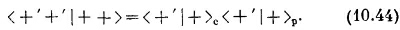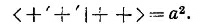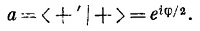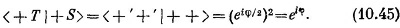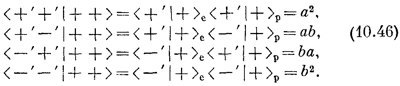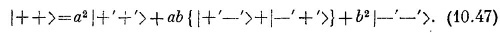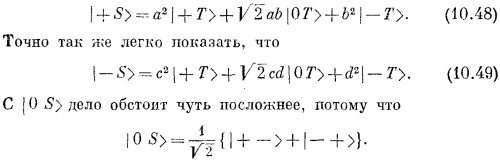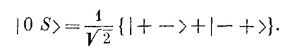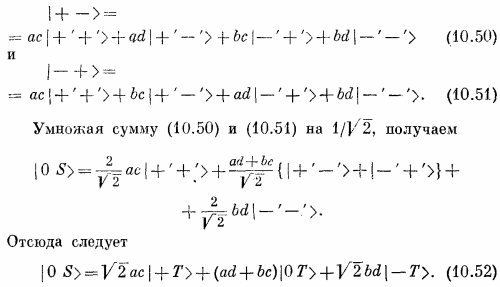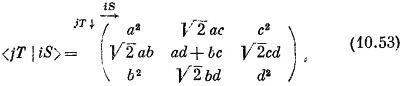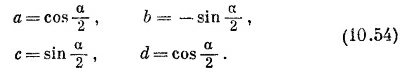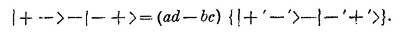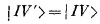Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 10. Сверхтонкое расщепление в водороде

Проекционная матрица для спина 1

Теперь мы хотели бы применить наши знания об атоме водорода к одной специальной задаче. В гл. 3 мы говорили о том, что частица со спином 1, находящаяся в одном из базисных состояний (+, 0, —) по отношению к прибору Штерна — Герлаха с какой-то частной ориентацией (скажем, по отношению к прибору S), будет иметь определенную амплитуду пребывания в одном из трех состояний по отношению к прибору Т, ориентированному в пространстве по-другому. Имеются девять таких амплитуд <jT |¡S>, которые вместе образуют проекционную матрицу. В гл. 3, § 7, мы без доказательства выписали элементы этой матрицы для различных ориентации Т по отношению к S. Теперь мы хотим показать вам один из способов их вывода.
 
В атоме водорода мы с вами отыскали систему со спином 1, составленную из двух частиц со спином ¹/₂. В гл. 4 мы уже научились преобразовывать амплитуды для спина ¹/₂. Эти знания можно применить к тому, чтобы получить преобразование для спина 1. Вот как это делается: имеется система (атом водорода с энергией +А) со спином 1. Пусть мы пропустили ее сквозь фильтр S Штерна — Герлаха так, что знаем теперь, что она находится в одном из базисных состояний по отношению к S, скажем в| +Sy. Какова амплитуда того, что она окажется в одном из базисных состояний, скажем | +T>, по отношению к прибору Т? Если вы назовете систему координат прибора S системой х, у, z, то состояние | +S> — это то, что недавно называлось состоянием | + +>. Но представьте, что какой-то ваш приятель провел свою ось z вдоль оси Т. Он свои состояния будет относить к некоторой системе х′ , у′, z′ . Его состояния «вверх» и «вниз» для электрона и протона отличались бы от ваших. Его состояние «плюс — плюс», которое можно записать | +′ + ′ >, отмечая «штрихованностъ» системы, есть состояние | + Т > частицы со спином 1. А вас интересует <+Т | +S>, что есть просто иной способ записи амплитуды <+′ + ′ I + +>.
 
Амплитуду <+′ + ′ I + +> можно найти следующим образом. В вашей системе спин электрона из состояния I + +> направлен вверх. Это означает, что у него есть некоторая амплитуда <+′ | + >_е оказаться в системе вашего приятеля спином вверх и некоторая амплитуда <–′ | + >_е оказаться в этой системе спином вниз. Равным образом, протон в состоянии ++>. У имеет спин вверх в вашей системе и амплитуды <+′ | + >_Р и <–′ | + >_Р оказаться спином вверх или вниз в «штрихованной» системе. Поскольку мы говорим о двух разных частицах, то амплитуда того, что обе частицы вместе в его системе окажутся спинами вверх, равна произведению амплитуд

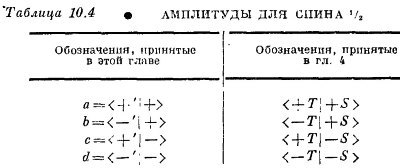
Мы поставили значки е и р под амплитудами <+′ I +>, чтоб было ясно, что мы делаем. Но обе они — это просто амплитуды преобразований для частицы со спином ¹/₂, так что на самом деле — это одни и те же числа. Фактически — это те же амплитуды, которые мы в гл. 4 называли <+T | +S> и которые мы привели в табл. 4.1 и 4.2.
 
Но теперь, однако, нам угрожает путаница в обозначениях. Надо уметь различать амплитуду < +Т | +S>  для частицы со спином ¹/₂ от того, что мы также назвали < +Т | +S>, но для спина 1—между ними нет ничего общего! Надеюсь, вас не очень собьет с толку, если мы на время введем иные обозначения амплитуд для спина ¹/₂,. Они приведены в табл. 10.4. Для состояний частиц спина 1 мы по-прежнему будем прибегать к обозначениям | +S>, | 0 S> и | — S>.

В наших новых обозначениях (10.44) просто превращается в

Это как раз амплитуда <+T | +S> для спина 1. Теперь давайте, например, предположим, что у вашего приятеля система координат, т. е. «штрихованный» прибор Т, повернута вокруг вашей оси z на угол φ; тогда из табл. 4.2 получается

Значит, из (10.44) амплитуда для спина 1 окажется равной

Теперь вам понятно, как мы будем действовать дальше.
 
Но хорошо бы провести выкладки в общем случае для всех состояний. Если протон и электрон в нашей системе (системе S) оба смотрят вверх, то амплитуды того, что в другой системе (системе Т) они будут в одном из четырех возможных состояний, равны

Затем мы можем записать состояние | ++ > в виде следующей линейной комбинации:

Но теперь мы замечаем, что | +′+′> —это состояние |+Т>, что {| +′–′> + | –′+′>} — это как раз √2,  умноженный на состояние |0T> [см.  (10.41)],   и что  |–′–′>= |–T>. Иными словами,  (10.47) переписывается в виде

S |0 S> дело обстоит чуть посложнее, потому что

Но каждое из состояний   | +– > и | –+ > можно   выразить через «штрихованные» состояния и подставить в сумму:

Теперь у нас есть все необходимые амплитуды. Коэффициенты в (10.48), (10.49) и (10.52) — это матричные элементы <jT I iS>. Сведем их в одну матрицу:

Мы выразили преобразование спина 1 через амплитуды а, b, с и d  преобразования спина ¹/₂.
 
Если, например, система Т повернута но отношению к S на угол α вокруг оси у (см. фиг. 3.6, стр. 64), то амплитуды в табл. 10.4 —это просто матричные элементы R_y (α) в табл. 4.2:

Подставив  их  в  (10.53),  получим формулы (3.38), которые приведены на стр. 80 без доказательства.
 
Но что же случилось с состоянием | /V>?! Это система со спином нуль; значит, у нее есть только одно состояние — оно во всех системах координат одно и то же. Можно проверить, что все так и выходит, если взять разность (10.50) и (10.51); получим

Но  (ad — bc) — это определитель матрицы для спина ¹/₂,  он просто равен единице. Получается

при любой относительной ориентации двух систем координат.

СМОТРИТЕ ТАКЖЕ: