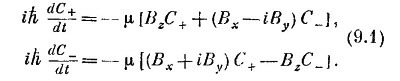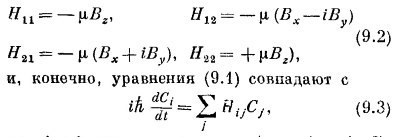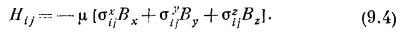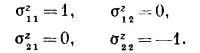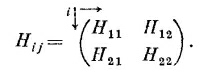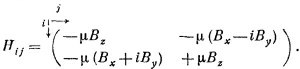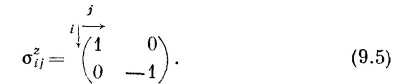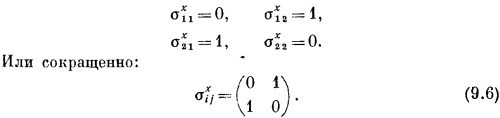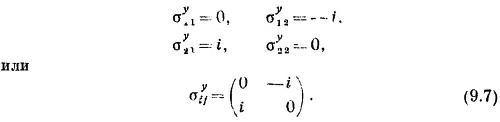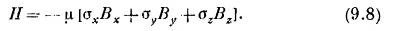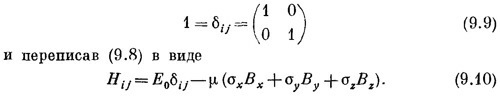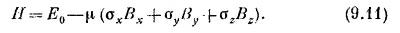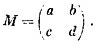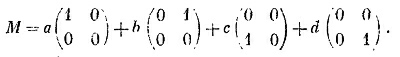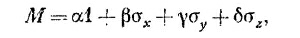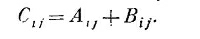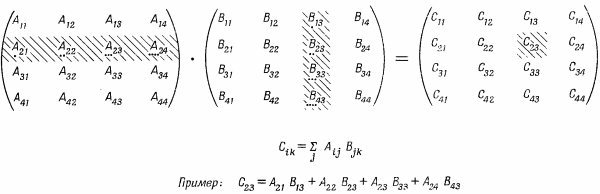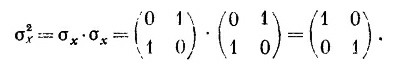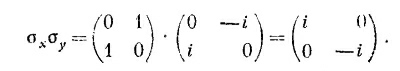Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 9. Еще системы с двумя состояниями

Спиновые матрицы Паули

Продолжаем обсуждение свойств двухуровневых систем. В конце предыдущей главы мы говорили о частице со спином ¹/₂ в магнитном поле. Мы описывали спиновое состояние, задавая амплитуду С₁ того, что z-компонента спинового момента количества движения равна + h/2, и амплитуду С₂ того, что она равна —h/2. В предыдущих главах мы эти базисные состояния обозначали | +> и | –>. Прибегнем опять к этим обозначениям, хотя, когда это будет удобнее, мы будем менять их на  | 1> и | 2>.
 
Мы видели в последней главе, что когда частица со спином ¹/₂ и с магнитным моментом μ находится в магнитном поле В=(B_х, B_y, B_z), то амплитуды С₊ (=С₁) и С_ ( = С₂) связаны следующими дифференциальными уравнениями:

Иначе говоря,  матрица-гамильтониан  H_¡j имеет вид

где i и j принимают значения +  и — (или 1 и 2).
 
Эта система с двумя состояниями — спин электрона — настолько важна, что очень полезно было бы найти для ее описания способ поаккуратнее и поизящнее. Мы сейчас сделаем небольшое математическое отступление, чтобы показать вам, как обычно пишутся уравнения системы с двумя состояниями. Это делается так: во-первых, заметьте, что каждый член гамильтониана пропорционален μ и некоторой компоненте В; поэтому (чисто формально) можно написать

Здесь нет какой-либо новой физики; эти уравнения просто означают, что коэффициенты σ^x_¡j, σ^y_¡j и σ^z_¡j — их всего 4Х 3 = 12 — могут быть представлены так, что (9.4) совпадет с (9.2).
 
Посмотрим, почему это так. Начнем с B_z. Раз B_z встречается только в H₁₁ и Н.₂₂, то все будет в порядке, если взять

Мы часто пишем  матрицу  Н_¡j в виде  таблички такого рода:

Для гамильтониана частицы со спином ¹/₂ в магнитном  поле В —это все равно что

Точно так же и коэффициенты σ^z_¡j   можно записать в виде матрицы

Расписывая коэффициенты при В_х, получаем, что элементы матрицы σ_х должны иметь вид

И наконец, глядя на В , получаем

Если так определить три матрицы сигма, то уравнения (9.1) и (9.4) совпадут. Чтоб оставить место для индексов i и j, мы отметили, какая σ стоит при какой компоненте В, поставив индексы х, y, z сверху. Обычно, однако, i и j отбрасывают (их легко себе и так вообразить), а индексы х, у и z ставят внизу. Тогда (9.4) записывается  так:

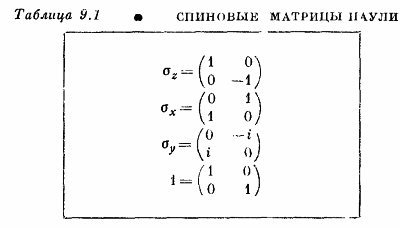
Матрицы сигма так важны (ими беспрерывно пользуются), что мы выписали их в табл. 9.1. (Тот, кто соиирается работать в квантовой физике, обязан запомнить их.) Их еще называют спиновыми матрицами Паули — по имени физика, который их выдумал.

В таблицу мы включили еще одну матрицу 2x2, которая бывает нужна тогда, когда мы хотим рассматривать систему, оба спиновых состояния которой имеют одинаковую энергию, или когда хотим перейти к другой нулевой энергии. В таких случаях к первому уравнению в (9.1) приходится добавлять Е₀С ₊ , а ко второму Е₀С _. Это можно учесть, введя новое обозначение — единичную матрицу «1», или δ_¡j:

Обычно просто понимают без лишних оговорок, что любая константа наподобие Е₀ автоматически умножается на единичную матрицу, и тогда пишут просто

Одна из причин, отчего спиновые матрицы так полезны,— это что любая матрица 2x2 может быть выражена через них. Во всякой матрице стоят четыре числа, скажем

Ее всегда можно записать в виде  линейной комбинации четырех матриц. Например,

Это можно делать по-всякому, но, в частности, можно сказать, что М состоит из какого-то количества σ_х плюс какое-то количество σ_y  и т, д., и написать

где «количества» α, β, γ и δ в общем случае могут быть комплексными числами.
 
Раз любая матрица 2x2 может быть выражена через единичную матрицу и матрицу сигма, то все, что может понадобиться для любой системы с двумя состояниями, у нас уже есть. Какой бы ни была система с двумя состояниями — молекула аммиака, краситель фуксии, что угодно,— гамильтоново уравнение может быть переписано в сигмах. Хотя в физическом случае электрона в магнитном поле сигмы кажутся имеющими геометрический смысл, но их можно считать и просто полезными матрицами, пригодными к употреблению во всякой системе с двумя состояниями.
 
Например, один из способов рассмотрения протона и нейтрона — это представлять их как одну и ту же частицу в любом из двух состояний. Мы говорим, что нуклон (протон или нейтрон) есть система с двумя состояниями, в данном случае состояниями по отношению к электрическому заряду. Если рассматривать нуклон таким образом, то состояние |1> может представлять протон, а |2> —нейтрон. Говорят, что у нуклона есть два состояния   «изотопснина».
 
Поскольку мы будем применять матрицы сигма в качестве «арифметики» квантовой механики систем с двумя состояниями, то наскоро познакомимся с соглашениями матричной алгебры. Под «суммой» двух или большего числа матриц подразумевается как раз то,  что  имелось  в  виду  в уравнении   (9.4). Вообще если мы «складываем» две матрицы А и В, то «сумма» С означает,  что каждый ее элемент С_¡j дается формулой

Каждый элемент С есть сумма элементов А и В, стоящих на тех же самых местах.
 
В гл. 3, § 6, мы уже сталкивались с представлением о матричном «произведении». Та же идея полезна и при обращении с матрицами сигма. В общем случае «произведение» двух матриц А и В (в этом именно порядке) определяется как матрица С с элементами

Это — сумма произведений элементов, взятых попарно из ¡-й строчки А и k-го столбца В. Если матрицы расписаны в виде таблиц, как на фиг. 9.1, то можно указать удобную «систему» получения элементов матрицы-произведения. Скажем, вы вычисляете С₂₃. Вы двигаете левым указательным пальцем по второй строчке А, а правым — вниз по третьему столбцу В, перемножаете каждую пару чисел и складываете пары по мере движения. Мы попытались изобразить это на рисунке.

Для матриц 2x2 ото выглядит особенно просто. Например, если σ_х умножается на σ_х, то выходит

т. е. просто единичная матрица. Или. для примера, подсчитаем еще

Взглянув на табл. 9.1, вы видите, что это просто матрица σ_x, умноженная на i. (Вспомните, что умножение матрицы на число означает умножение каждого элемента матрицы на число.) Попарные произведения сигм очень важны и выглядят они довольно забавно, так что мы их выписали в табл. 9.2. Вы сами можете подсчитать их, как мы сделали это с σ_x² и σ_xσ_y.

С матрицами σ связан еще один очень интересный и важный момент. Можно, если угодно, представить себе, что три матрицы σ_х, σ_у и σ_z подобны трем компонентам вектора; его иногда именуют «вектором сигма» и обозначают σ. Это на самом деле «матричный вектор», или «векторная матрица». Это три разные матрицы, связанные каждая со своей осью х, у или z. С их помощью гамильтониан системы можно записать в красивом виде, пригодном для любой системы координат:

Хотя мы записали эти три матрицы в представлении, в котором понятия «вверх» и «вниз» относятся к направлению z (так что σ_z выглядит особенно просто), но можно представить себе, как будут они выглядеть в любом другом представлении. И хотя это требует немалых выкладок, можно все же показать, что они изменяются как компоненты вектора. (Мы, впрочем, пока не будем заботиться о том, чтобы доказать это. Проверьте сами, если хотите.) Вы можете пользоваться σ в различных системах координат, как если бы это был вектор.
 
Вы помните, что гамильтониан H связан в квантовой механике с энергией. Он действительно в точности совпадает с энергией в том простом случае, когда состояний только одно. Даже в системе с двумя состояниями, какой является спин электрона, если записать гамильтониан в виде (9.13), он очень напоминает классическую формулу энергии магнита с магнитным моментом ,и в магнитном поле В. Классически это выглядит так:

где μ — свойство объекта, а В — внешнее поле. Можно вообразить себе, что (9.14) обращается в (9.13), если классическую энергию заменяют гамильтонианом, а классическое μ — матрицей μσ. Тогда после такой чисто формальной замены результат можно будет интерпретировать как матричное уравнение. Иногда утверждают, что каждой величине в классической физике соответствует в квантовой механике матрица. На самом деле правильнее было бы говорить, что матрица Гамильтона соответствует энергии и что у каждой величины, которая может быть определена через энергию, есть соответствующая матрица. Например, магнитный момент можно определить через энергию, сказав, что энергия но внешнем поле В есть —μ·В. Это определяет вектор магнитного момента μ. Затем мы смотрим на формулу для гамильтониана реального (квантового) объекта в магнитном поле и пытаемся угадать, какие матрицы соответствуют тем или иным величинам в классической формуле. С помощью этого трюка иногда у некоторых классических величин появляются их квантовые двойники.
 
Если хотите, попробуйте разобраться в том, как, в каком смысле классический вектор равен матрице μσ: может быть, вы что-нибудь и откроете. Но не надо ломать над этим голову. Право же, не стоит: на самом-то деле они не равны. Квантовая механика — это совсем другой тип теории, другой тип представлений о мире. Иногда случается, что всплывают некоторые соответствия, но вряд ли они представляют собой нечто большее, нежели мнемонические средства -- правила для запоминания.
 
Иначе говоря, вы запоминаете (9.14), когда учите классическую физику; затем если вы запомнили соответствие μ →μσ, то у вас есть повод вспомнить (9.13). Разумеется, природа знает квантовую механику, классическая же является всего лишь приближением, значит, нет ничего загадочного в том, что из-за классической механики выглядывают там и сям тени квантовомеханичееких законов, представляющих на самом деле их подоплеку. Восстановить реальный объект по тени прямым путем никак невозможно, но тень помогает нам вспомнить, как выглядел объект. Уравнение (9.13) — это истина, а уравнение (9.14) — ее тень. Мы сперва учим классическую механику и поэтому нам хочется выводить из нее квантовые формулы, но раз и навсегда установленной схемы для этого нет. Приходится каждый раз возвращаться обратно к реальному миру и открывать правильные квантовомеханические уравнения. И когда они оказываются похожими на что-то классическое, мы радуемся.
 
Если эти предостережения покажутся вам надоедливыми, если, по-вашему, здесь изрекаются старые истины об отношении классической физики к квантовой, то прошу прощения: сработал условный рефлекс преподавателя, который привык втолковывать квантовую механику студентам, никогда прежде не слыхавшим о спиновых матрицах Паули. Мне всегда казалось, что они не теряют надежды, что квантовая механика как-то сможет быть выведена как логическое следствие классической механики, той самой, которую они старательно учили в прежние годы. (Может быть, они просто хотят обойтись без изучения чего-то нового.) Но, к счастью, вы выучили классическую формулу (9.14) всего несколько месяцев тому назад, да и то с оговорками, что она не совсем правильна, так что, может быть, вы не будете столь неохотно воспринимать необходимость рассматривать квантовую формулу (9.13) в качестве первичной истины.

СМОТРИТЕ ТАКЖЕ: