Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 8. Другие системы с двумя состояниями Вращающийся электрон в магнитном поле
Пример первый: пусть сначала имеется постоянное ноле в направлении z. Ему соответствуют два стационарных состояния с энергиями ±μBz. Добавим небольшое поле в направлении х. Тогда уравнения получатся такими же, как в нашей старой задаче о двух состояниях. Опять, в который раз, получается знакомый уже нам переброс, и уровни энергии немного расщепляются. Пусть, далее, х-компонента поля начнет меняться во времени, скажем, как cos ωt. Тогда уравнения станут такими, как для молекулы аммиака в колеблющемся электрическом поле (см. гл. 7). И тем же способом, что и прежде, вы можете рассчитать процесс во всех деталях. При этом вы увидите, что колеблющееся поле приводит к переходам от + z-состояния к —z-состоянию я обратно, если только горизонтальное поле колеблется с частотой, близкой к резонансной, ω0=2μBz/h. Это приводит к квантовомеханической теории явлений магнитного резонанса, описанной нами в гл. 35 (вып. 7).
 Можно еще сделать мазер, в котором используется система со спином 1/2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении + z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнитным моментом, вызовут переходы, которые будут снабжать полость энергией. Можно еще сделать мазер, в котором используется система со спином 1/2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении + z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнитным моментом, вызовут переходы, которые будут снабжать полость энергией.
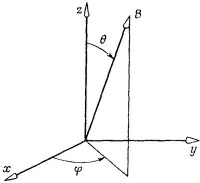
Рассмотрим теперь второй пример. Пусть у нас имеется магнитное поле В, направление которого характеризуется полярным углом θ и азимутальным углом φ (фиг. 8.10). Допустим еще, что имеется электрон, спин которого направлен по нолю. Чему равны амплитуды С1 и С2 для этого электрона? Иными словами, обозначая состояние электрона | ψ>, мы хотим написать
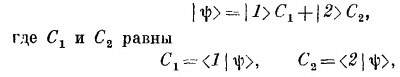 |
а | 1> и | 2> обозначают то же самое, что раньше обозначалось | + > и | –> (по отношению к выбранной нами оси z).
Ответ на этот вонрос также содержится в наших общих уравнениях для систем с двумя состояниями. Во-первых, мы знаем, что раз спин электрона параллелен В, то электрон находится в стационарном состоянии с энергией ЕI= — μВ. Поэтому и С1, и С2 должны изменяться как е –iEII/h [см.. уравнение (7.18)] ; и их коэффициенты а1 и а2 даются формулой (8.5):
Вдобавок а1 и а2 должны быть нормированы так, чтобы было | а1 |2 + | a2 |2 =1. Величины Н11 и H12 мы можем взять из (8.22), используя равенства
Кстати, скобка во втором уравнении есть просто е–¡φ, так что проще писать
Подставляя эти матричные элементы в (8.24) и сокращая на —μB, находим
Зная это отношение и зная условие нормировки, можно найти и a1 и а2. Сделать это нетрудно, но мы сократим путь, прибегнув к одному трюку. Известно, что 1—cosθ = 2sin2 (θ/2) и sinθ = 2sin(θ/2)cos(θ/2). Значит, (8.27) совпадает с
Один из ответов, следовательно, таков:
Он удовлетворяет и уравнению (8.28), и условию
Вы знаете, что умножение а1 и a2 на произвольный фазовый множитель ничего не меняет. Обычно формуле (8.29) предпочитают более симметричную запись, умножая на e¡φ/2. Принято писать так:
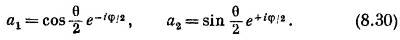 |
Это и есть ответ на наш вопрос. Числа а1 и а2 — это амплитуды того, что электрон будет замечен спином вверх или вниз (по отношению к оси z), если известно, что его спин направлен вдоль оси (θ, φ). [Амплитуды С1 и С2 равны просто а1 и a2, умноженным на e–¡EIth.]
Заметьте теперь занятную вещь. Напряженность В магнитного поля нигде в (8.30) не появляется. Тот же результат, разумеется, получится в пределе, если поле В устремить к нулю. Это означает, что мы дали общий ответ на вопрос, как представлять частицу, спин которой направлен вдоль произвольной оси. Амплитуды (8.30) — это проекционные амплитуды для частиц со спином 1/2, подобные проекционный амплитудам для частиц со спином 1. приведенным в гл. 3 [уравнения (3.38)]. Теперь мы сможем находить для фильтрованных пучков частиц со спином 1/2 амплитуды проникновения через тот или иной фильтр Штерна — Герлаха.
Пусть |+z> представляет состояние со спином, направленным по оси z вверх, а | – z> — состояние со спином вниз. Если | +z′> представляет состояние со спином, направленным вверх по оси z′, образующей с осью z углы θ и φ, то в обозначениях гл. 3 мы имеем
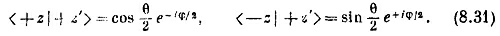 |
Эти результаты эквивалентны тому, что мы нашли из чисто геометрических соображений в гл. 4 [уравнение (4.36)]. (Если вы в свое время решили пропустить гл. 4, то вот перед вами один из ее существенных результатов.)
Напоследок вернемся еще раз к тому примеру, о котором уже не раз говорилось. Рассмотрим такую задачу. "Сперва имеется электрон с определенным образом направленным спином, затем на 25 минут включается магнитное поле в направлении z, а затем выключается. Каким окажется конечное состояние? Опять представим состояние в виде линейной комбинации | ψ> = |1> C1+ |2> C2. Но в нашей задаче состояния с определенной энергией являются одновременно нашими базисными состояниями | 1> и |2>. Значит, C1 и С2 меняются только по фазе. Мы знаем, что
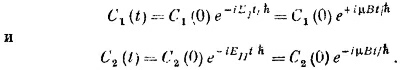 |
Мы сказали, что вначале у спина электрона было определенное направление. Это означает, что вначале С1 и С2 были двумя числами, определяемыми формулами (8.30). Переждав Т секунд, новые C1 и C2 мы получим из прежних умножением соответственно на eiμBzT/ h e–iμBzT/ h. Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол φ, вычтя из него 2μBzT/h, и не трогать угол θ.
Это значит, что к концу интервала времени Т состояние |ψ > будет представлять электрон, выстроенный в направлении, отличающемся от первоначального только поворотом вокруг оси z на угол Δφ=2μВzT/h. Раз этот угол пропорционален Т, то можно говорить, что направление спина прецессирует вокруг оси z с угловой скоростью 2μВz/h. Этот результат мы уже получали раньше несколько раз, но не так полно и строго. Теперь мы получили полное и точное квантовомеханическое описание прецессии атомных магнитов.
Любопытно, что математические идеи, которые мы только что применили к электрону, вращающемуся в магнитном поле, применимы и для любой системы с двумя состояниями. Это означает, что, проведя математическую аналогию с вращающимся электроном, можно при помощи чисто геометрических рассуждений решить любую задачу для двухуровневой системы. Сперва вы сдвигаете энергию так, чтобы (Н11+ Н22) было равно нулю (так что Н11= — Н22). И тогда любая задача о такой системе формально совпадет с задачей об электроне в магнитном поле. Вам нужно будет только отождествить —μВz с H11, а —μ(Вх — iBy ) с H12. И неважно, какая физика там была первоначально — молекула ли аммиака или что другое, — вы можете перевести ее на язык соответствующей задачи об электроне. Стало быть, если мы в состоянии решить в общем случае задачу об электроне, мы уже решили все задачи о двух состояниях.
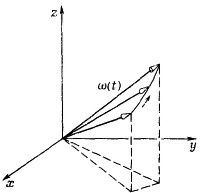 А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью ω (t), равной некоторой константе, умноженной на вектор В (а именно ω= 2μВ/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11). Если все время это делать, вы остановитесь на какой-то конечной ориентации спиновой оси, и амплитуды С1 и С2 получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат. А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью ω (t), равной некоторой константе, умноженной на вектор В (а именно ω= 2μВ/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11). Если все время это делать, вы остановитесь на какой-то конечной ориентации спиновой оси, и амплитуды С1 и С2 получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.
Вы видите, что задача эта чисто геометрическая: надо заметить, где закончились все ваши вращения. Хотя сразу видно, что для этого требуется, но эту геометрическую задачу (отыскание окончательного итога вращений с переменным вектором угловой скорости) нелегко в общем случае решить явно. Во всяком случае, мы в принципе видим общее решение любой задачи для двух состояний. В следующей главе мы глубже исследуем математическую технику обращения с частицами спина 1/2 и, следовательно, обращения с системами, обладающими двумя состояниями, в общем случае.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Можно еще сделать мазер, в котором используется система со спином 1/2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении + z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнитным моментом, вызовут переходы, которые будут снабжать полость энергией.
Можно еще сделать мазер, в котором используется система со спином 1/2. Прибор Штерна — Герлаха создает пучок частиц, поляризованных, скажем, в направлении + z, и они потом направляются в полость, находящуюся в постоянном магнитном поле. Колеблющиеся в полости поля, взаимодействуя с магнитным моментом, вызовут переходы, которые будут снабжать полость энергией.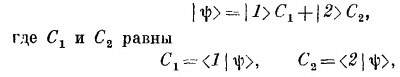

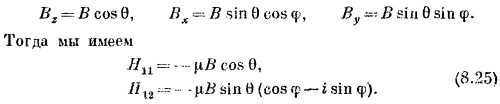
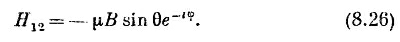


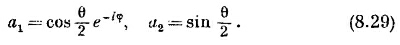
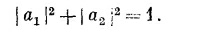
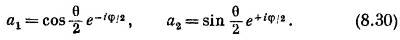
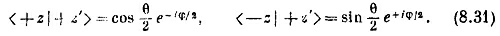
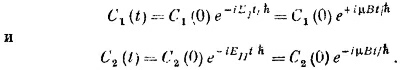
 А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью ω (t), равной некоторой константе, умноженной на вектор В (а именно ω= 2μВ/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11). Если все время это делать, вы остановитесь на какой-то конечной ориентации спиновой оси, и амплитуды С1 и С2 получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.
А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью ω (t), равной некоторой константе, умноженной на вектор В (а именно ω= 2μВ/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11). Если все время это делать, вы остановитесь на какой-то конечной ориентации спиновой оси, и амплитуды С1 и С2 получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.