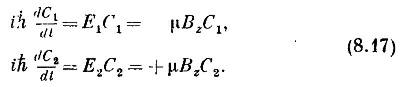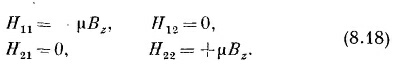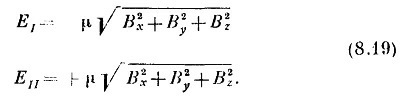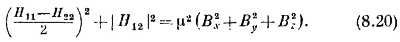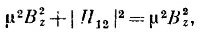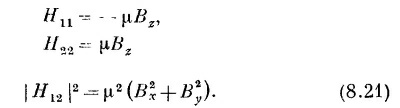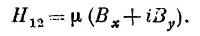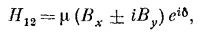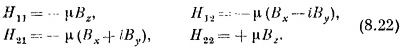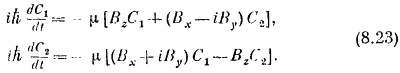| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Гамильтониан частицы со спином 1/2 в магнитном поле
Обратимся теперь еще к одной системе с двумя состояниями. На этот раз нашим объектом будет частица со спином 1/2. Кое-что из того, что мы намерены сказать, затрагивалось уже в предыдущих главах, но повторение поможет нам немного прояснить кое-какие темные места. Покоящийся электрон мы можем считать тоже системой с двумя состояниями. Хотя в этом параграфе мы будем толковать об «электроне», но то, что мы выясним, будет справедливо по отношению ко всякой частице со спином 1/2.
В этом частном случае гамильтониан равен
Итак, мы знаем, какой вид имеет гамильтониан, когда магнитное поле направлено по z, и знаем еще энергии стационарных состояний.
Дальше все уже совсем легко. У нас есть формулы для энергий. Нам нужен гамильтониан, линейный по Вх, Вy и Вz, который даст именно такие энергии, если применить нашу общую формулу (8.3). Задача — найти гамильтаниан. Прежде всего заметим, что энергия расщепляется симметрично и ее среднее значение есть нуль. Взглянув на (8.3), мы сразу же увидим, что для этого требуется
(Заметьте, что это подтверждается тем, что нам уже известно при Bx=By=0; в этом случае H11 = —μBz и H22 — μBz.) Если теперь приравнять энергии из (8.3) к тому, что нам известно из (8.19), то получится
(Мы использовали также тот факт, что H21=H12, Tак что H12H21 может быть записано в виде | Н12 |2.) Опять в частном случае поля в направлении z это даст
откуда | H12 | в этом частном случае равно нулю, что означает, что в H12 не может войти член с Bz. (Вы помните, что мы говорили о линейности всех членов по Вх, Вy и Вz.)
Оказывается, что никак иначе этого сделать нельзя!
На самом деле таких возможностей не одна, в общем случае можно написать
где δ — произвольная фаза.
(Кстати, эти соглашения связаны и согласуются с тем произволом в выборе фаз, который мы использовали в гл. 4.) Полный гамильтониан для электрона в произвольном магнитном поле, следовательно, равен
А уравнения для амплитуд C1 и C2 таковы:
Итак, мы открыли «уравнения движения спиновых состояний» электрона в магнитном поле. Мы угадали их, пользуясь некоторыми физическими аргументами, но истинная проверка всякого гамильтониана заключается в том, что он обязан давать предсказания, согласующиеся с экспериментом. Из всех сделанных проверок следует, что эти уравнения правильны. Более того, хотя все наши рассуждения относились к постоянному полю, написанный нами гамильтониан правилен и тогда, когда магнитные поля меняются со временем. Значит, мы теперь можем применять уравнения (8.23) для решения всевозможных интересных задач. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.