| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Молекула в статическом электрическом поле
Если молекула аммиака находится в любом из двух состояний определенной энергии, а мы приложим к ней возмущение с частотой ω, такой, что hω=EI—ЕII=2А, то система может перейти из нижнего состояния в верхнее. Или она может перейти из верхнего в нижнее и испустить фотон. Но для возбуждения таких переходов у вас должна быть физическая связь с состояниями — возможность возмущать систему. Должен существовать какой-то внешний механизм влияния на состояния, нечто вроде электрического или магнитного поля. В нашем частном случае эти состояния чувствительны к электрическому полю. На очереди, стало быть, у нас теперь проблема поведения молекулы аммиака во внешнем электрическом поле.
Кроме того, предположим, что при интересующих нас электрических полях сами поля не сказываются заметно на геометрии молекулы и, стало быть, на амплитуде того, что атом азота перепрыгнет из одного положения в другое. Поэтому можно принять, что Н12 и Н21 не изменились, т. е.
Теперь с этими новыми значениями Hij надо решать гамильтоновы уравнения (6.43). Мы могли бы их решить просто, как делали это прежде, но поскольку нам не раз, видимо, представится случай решать системы с двумя состояниями, то давайте уж решим их раз и навсегда в общем случае произвольного Hij, считая только, что со временем оно не меняется.
Это линейные дифференциальные уравнения с постоянными коэффициентами. Значит, всегда можно найти решения, являющиеся экспоненциальными функциями независимой переменной t. Сперва отыщем решения, в которых С1 и С2 одинаково зависят от времени; возьмем пробные функции
Поскольку это решение отвечает состоянию с энергией Е=hω, то можно прямо написать
где Е пока неизвестна и должна быть определена так, чтобы дифференциальные уравнения (7.16) и (7.17) выполнялись. При подстановке С1 и С2 из (7.18) и (7.19) в дифференциальные уравнения (7.16) и (7.17) производные дают просто —iE/h, умноженное на С1 или С2, так что слева остается попросту ЕС1 или ЕС2. Сокращая общие экспоненциальные множители, получаем
или после перестановки членов
У такой системы однородных алгебраических уравнений ненулевые решения для а1 и а2 будут лишь тогда, когда определитель, составленный из коэффициентов при а1 и а2, равен нулю, т. е. если
Но когда уравнений два и неизвестных тоже два, то можно обойтись и без столь возвышенных представлений. Каждое из уравнений (7.20) и (7.21) дает отношение двух коэффициентов а1 и а2, и эти два отношения должны быть равны. Из (7.20) мы имеем
Приравнивая эти отношения, получаем, что Е должно удовлетворять равенству
То же получилось бы и из (7.22). В любом случае для Е получается квадратное уравнение с двумя регистрами:
Энергия Е может иметь, два значения. Заметьте, что оба они вещественны, потому что Н11 и Н22 вещеетвенны, а Н 1гН21. равное Н12Н12 = | H12 |2, тоже вещественно, да к тому же положительно.
Подставив каждую из этих анергий по отдельности в (7.18) и (7.19), получим амплитуды для двух стационарных состояний (состояний определенной энергии). Если нет каких-либо внешних возмущений, то система, первоначально бывшая в одном из этих состояний, останется о нем навсегда, у нее только фаза будет меняться.
В общем случае два решения ЕI и EII относятся к двум состояниям; мы их опять можем назвать состояниями
У этих состояний С1 и С2 будут даваться уравнениями (7.18) и (7.19), где а1 и а2 еще подлежат определению. Их отношение дается либо формулой (7.23), либо (7.24). Они должны также удовлетворять еще одному условию. Если известно, что система находится в одном из стационарных состояний, то сумма вероятностей того, что она окажется в |1 > или |2>, должна равняться единице. Следовательно,
Эти условия не определяют а1 и а2 однозначно: остается еще произвол в фазе, т. е. в множителе типа е¡δ. Хотя для а можно выписать общие решения, но обычно удобнее вычислять их в каждом отдельном случае.
Tom, факт, что у азота существует амплитуда переброса вверх — вниз, малосуществен, когда энергии в этих двух положениях сильно отличаются. Это интересный момент, к которому мы позже еще вернемся.
Во всех практических случаях энергетические уровни, стало быть, равны
и энергии с E2 меняются линейно. Действующая на молекулы сила тогда равна
Энергия в электрическом поле у многих молекул пропорциональна E2. Коэффициент — это поляризуемость молекулы. Поляризуемость аммиака необычно высока: у него А в знаменателе очень мало. Стало быть, молекулы аммиака очень чувствительны к электрическому полю. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

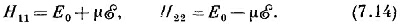

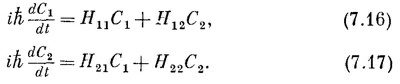



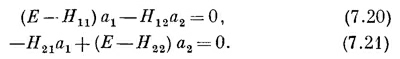
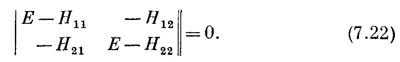
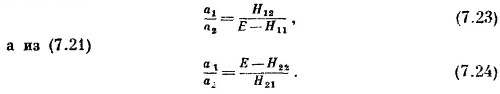
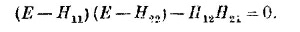
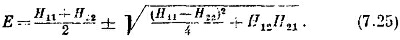
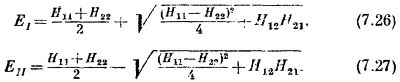
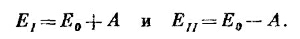
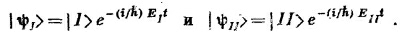
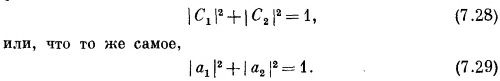
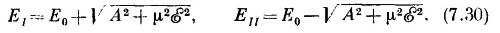
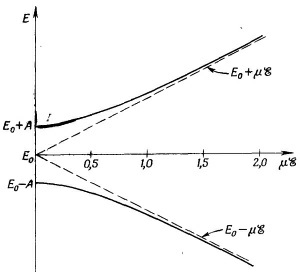 Эти две энергии как функции напряженности E электрического поля изображены на фиг. 7.2. Когда электрическое поле нуль, то энергии, естественно, обращаются в Е0±А. При наложении электрического поля расщепление уровней растет. Сперва при малых E оно растет медленно, но затем может стать пропорциональным E. (Эта линия — гипербола.) В сверхсильных полях энергии попросту равны
Эти две энергии как функции напряженности E электрического поля изображены на фиг. 7.2. Когда электрическое поле нуль, то энергии, естественно, обращаются в Е0±А. При наложении электрического поля расщепление уровней растет. Сперва при малых E оно растет медленно, но затем может стать пропорциональным E. (Эта линия — гипербола.) В сверхсильных полях энергии попросту равны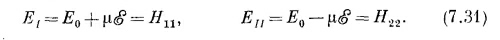
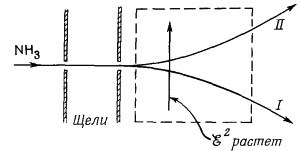 Как же разделить два молекулярных состояния? Один способ такой. Аммиачный газ выпускается тонкой струйкой и проходит через пару щелей, создающих узкий пучок (фиг. 7.3).
Как же разделить два молекулярных состояния? Один способ такой. Аммиачный газ выпускается тонкой струйкой и проходит через пару щелей, создающих узкий пучок (фиг. 7.3).