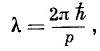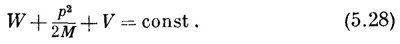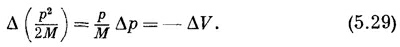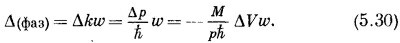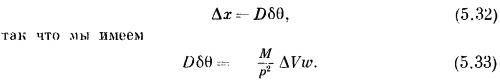| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Силы. Классический предел
Тогда угол отклонения δθ будет равен
где р — начальный импульс. Подставляя вместо F число —∂V/∂y, получаем
Теперь нам предстоит выяснить, удастся ли получить этот результат с помощью представления о том, что волны подчиняются уравнению (5.20). Мы рассмотрим то же самое явление квантовомеханически, предполагая, что все масштабы в нем намного превосходят длины волн наших амплитуд вероятности. В любой маленькой области можно считать, что амплитуда меняется как
где р связано с V формулой
В области, где V больше, там р меньше, а волны длиннее. Поэтому направление линий узлов волн постепенно меняется, как показано на рисунке.
Волновое число р/h поэтому тоже на разных путях различно, что означает, что фазы растут вдоль них с разной скоростью. Разница в скорости роста фазы есть Δk = Δp/h, и накопленная на всем пути w разность фаз будет равна
Это число показывает, на сколько к моменту выхода из полосы фаза вдоль пути b «опережает» фазу вдоль пути а. Но на выходе из полосы такое опережение фаз отвечает опережению узла волны на величину
или
Обращаясь к фиг. 5.8, мы видим, что новый фронт волны повернется на угол δθ, даваемый формулой
А это совпадает с (5.26), если заменить р/М на v, a ΔV/D на ∂V/∂y. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

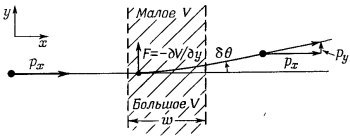 Предположим, что частица движется сквозь область, где есть потенциал, меняющийся поперек движения. Классически мы бы описали этот случай так, как показано на фиг. 5.7. Если частица движется в направлении х и вступает в область, где имеется потенциал, изменяющийся вдоль у, то частица получит поперечное ускорение от силы F= –∂V/∂y. Если сила присутствует только в ограниченной области шириной w, то она будет действовать только в течение времени w/v. Частица получит поперечный импульс
Предположим, что частица движется сквозь область, где есть потенциал, меняющийся поперек движения. Классически мы бы описали этот случай так, как показано на фиг. 5.7. Если частица движется в направлении х и вступает в область, где имеется потенциал, изменяющийся вдоль у, то частица получит поперечное ускорение от силы F= –∂V/∂y. Если сила присутствует только в ограниченной области шириной w, то она будет действовать только в течение времени w/v. Частица получит поперечный импульс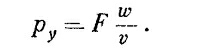
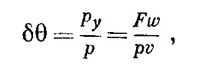

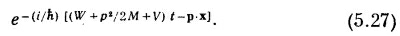
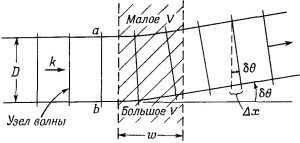 В состоянии ли мы увидеть, как отсюда получится отклонение частиц, когда у V будет поперечный градиент? На фиг. 5.8 мы прикинули, как будут выглядеть волны амплитуды вероятности Мы начертили ряд «узлов волн», которые вы можете считать, скажем, поверхностями, где фаза амплитуды равна нулю. В любой небольшой области длина волны (расстояние между соседними узлами) равна
В состоянии ли мы увидеть, как отсюда получится отклонение частиц, когда у V будет поперечный градиент? На фиг. 5.8 мы прикинули, как будут выглядеть волны амплитуды вероятности Мы начертили ряд «узлов волн», которые вы можете считать, скажем, поверхностями, где фаза амплитуды равна нулю. В любой небольшой области длина волны (расстояние между соседними узлами) равна