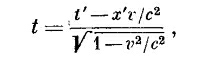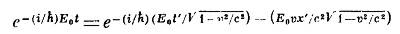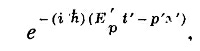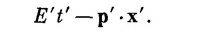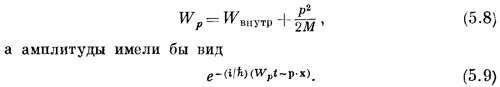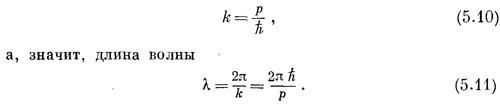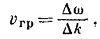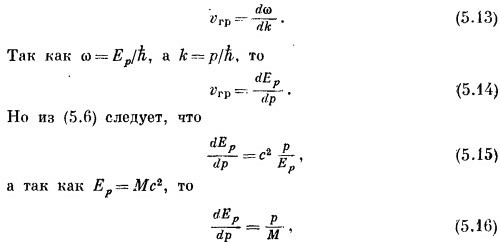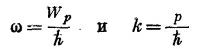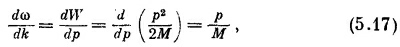| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Равномерное движение
и теперь наша амплитуда меняется так:
В штрихованной системе она меняется в пространстве и во времени. Если амплитуду записать в виде
то видно, что Е′р = E0/√1—v2/c2. Это энергия, вычисленная по классическим правилам для частицы с энергией покоя Е0, движущейся со скоростью v; p′= Е′рv/c2 — соответствующий импульс частицы.
Итак, амплитуда вероятности для частицы, импульс которой есть р, будет пропорциональна
где Ер— энергия частицы с импульсом р, т. е.
а Е0, как и прежде,—энергия покоя. В нерелятивистских задачах можно писать
где Wp— избыток (или нехватка) энергии по сравнению с энергией покоя Мsс2 частей атома. В общем случае в Wр должны были бы войти и кинетическая энергия атома, и его энергия связи или возбуждения, которые можно назвать «внутренней» энергией. Тогда мы бы писали
Мы собираемся все расчеты вести нерелятивистски, так что именно таким видом амплитуд вероятностей мы и будем пользоваться.
Это та самая длина волны, которую мы раньше использовали для частиц с импульсом р. Именно таким путем де-Бройль впервые пришел к этой формуле. Для движущейся частицы частота изменения амплитуды по-прежнему дается формулой
Абсолютная величина (5.9) равна просто единице, так что для частицы, движущейся с определенной энергией, вероятность обнаружить ее где бы то ни было — одна и та же повсюду и со временем не меняется. (Важно отметить, что амплитуда — это комплексная волна. Если бы мм пользовались вещественной синусоидой, то ее квадрат от точки к точке менялся бы, что было бы неверно.)
где Δk и Δω — разности волновых чисел и частот двух волн. В более сложных волнах, составленных из суммы многих амплитуд с близкими частотами, групповая скорость равна
а это как раз классическая скорость частицы. Даже применяя нерелятивистские выражения, мы будем иметь
т. е. опять классическую скорость. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

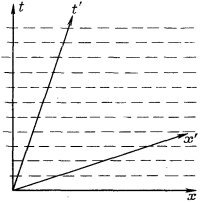 Если мы предполагаем, что теория относительности верна, то частица, покоящаяся в одной инерциальной системе, в другой инерциальной системе может оказаться в равномерном движении. В системе покоя частицы амплитуда вероятности для всех х, у и z одинакова, но зависит от t. Величина амплитуды для всех t одинакова, а фаза зависит от t. Мы можем получить картину поведения амплитуды, если проведем линии равной фазы (скажем, нулевой) как функций х и t. Для частицы в покое эти линии равной фазы параллельны оси х и расположены по оси t на равных расстояниях (показано пунктирными линиями на фиг. 5.1).
Если мы предполагаем, что теория относительности верна, то частица, покоящаяся в одной инерциальной системе, в другой инерциальной системе может оказаться в равномерном движении. В системе покоя частицы амплитуда вероятности для всех х, у и z одинакова, но зависит от t. Величина амплитуды для всех t одинакова, а фаза зависит от t. Мы можем получить картину поведения амплитуды, если проведем линии равной фазы (скажем, нулевой) как функций х и t. Для частицы в покое эти линии равной фазы параллельны оси х и расположены по оси t на равных расстояниях (показано пунктирными линиями на фиг. 5.1).