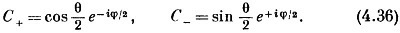| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Произвольные повороты
Итак, начав просто с некоторых предположений о свойствах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны амплитуды того, что любое состояние частицы со спином 1/2 перейдет в один из двух пучков прибора Штерна — Герлаха S с осями х, у, z, то мы можем подсчитать, какая часть перейдет в каждый пучок в приборе Т с осями x′, у′ и z′. Иначе говоря, если имеется состояние Ψ частицы со спином 1/2, у которого амплитуды пребывания вверху и внизу по отношению к оси z системы координат х, y, z равны С+=<+| Ψ> и С_ = <–|Ψ>, то тем самым мы знаем амплитуды С′+ и С′_ пребывания вверху и внизу по отношению к оси z′ любой другой системы x′, у′ и z′. Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином 1/2 в другие системы координат.
Вспоминая, что вначале было только одно состояние (+) по отношению к А, получаем
Мы хотели бы напоследок подытожить результаты этой главы в форме, которая окажется полезной для нашей дальнейшей работы. Во-первых, напомним, что наш основной результат (4.35) может быть записан в других обозначениях. Заметьте, что (4.35)— это то же самое, что и (4.4) Иначе говоря, в (4.35) коэффициенты при С+ = <+S |Ψ> и С_ = <–S |Ψ> суть как раз амплитуды <jT |iS> в (4.4), амплитуды того, что частица в состоянии i по отношению к S окажется в состоянии j по отношению к Т (когда ориентация Т по отношению к S дается углами α, β и γ). Мы их также называли RTSji в выражении (4.6). (Чего-чего, а обозначений у нас хватало!) Например, RTS_ + = < –T |S> — это коэффициент при С + в формуле для С′_ , а именно i sin(α/2) exp[ ¡(β—γ)/2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

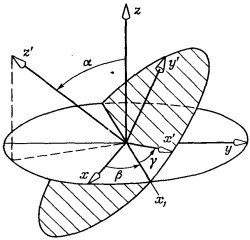 Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9). Если есть система осей х′, у′, z′ , ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера α, β и γ, определяющими три последовательных поворота, которые переводят систему х, у, z в систему х′, у′, z′ . Отправляясь от х, у, z, мы поворачиваем нашу систему на угол β вокруг оси z, перенося ось х на линию х′. Затем мы проводим поворот на угол α вокруг этой временной оси х1, чтобы довести ось z до z′. Наконец, поворот вокруг новой оси z (т. е. вокруг z′) на угол γ переведет ось х1 в х′, а ось у в у′. Мы знаем преобразования для каждого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем
Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9). Если есть система осей х′, у′, z′ , ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера α, β и γ, определяющими три последовательных поворота, которые переводят систему х, у, z в систему х′, у′, z′ . Отправляясь от х, у, z, мы поворачиваем нашу систему на угол β вокруг оси z, перенося ось х на линию х′. Затем мы проводим поворот на угол α вокруг этой временной оси х1, чтобы довести ось z до z′. Наконец, поворот вокруг новой оси z (т. е. вокруг z′) на угол γ переведет ось х1 в х′, а ось у в у′. Мы знаем преобразования для каждого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем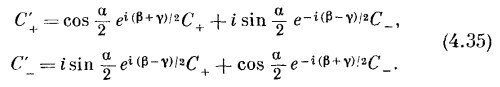
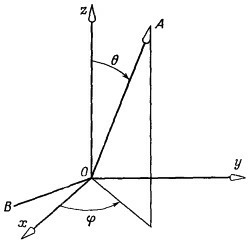 Вот еще пример. Пусть нам известно, что частица со спином 1/2 находится в состоянии Ψ, поляризованном вверх относительно оси А, определяемой углами θ и φ (фиг. 4.10). Мы хотим знать амплитуду < С+|Ψ > того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду < С_|Ψ > того, что она окажется в состоянии «вниз» относительно той же оси z. Эти амплитуды мы можем найти, вообразив, что А есть ось z′ системы, у которой ось х′ направлена произвольно, скажем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на —π/2 вокруг оси А, что переведет ось x в линию В на рисунке. Затем повернуть на — θ вокруг линии В (вокруг новой оси х′ системы А), чтобы ось А попала ни ось z. И, наконец, повернуть вокруг оси z на угол (π/2—φ).
Вот еще пример. Пусть нам известно, что частица со спином 1/2 находится в состоянии Ψ, поляризованном вверх относительно оси А, определяемой углами θ и φ (фиг. 4.10). Мы хотим знать амплитуду < С+|Ψ > того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду < С_|Ψ > того, что она окажется в состоянии «вниз» относительно той же оси z. Эти амплитуды мы можем найти, вообразив, что А есть ось z′ системы, у которой ось х′ направлена произвольно, скажем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на —π/2 вокруг оси А, что переведет ось x в линию В на рисунке. Затем повернуть на — θ вокруг линии В (вокруг новой оси х′ системы А), чтобы ось А попала ни ось z. И, наконец, повернуть вокруг оси z на угол (π/2—φ).