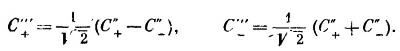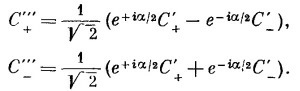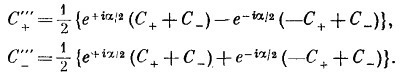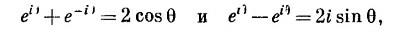| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
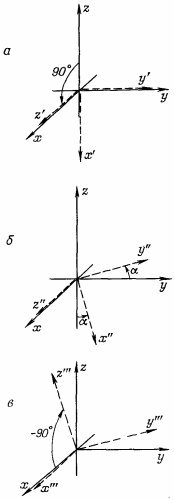
Повороты вокруг оси х
Последний поворот на —90° вокруг оси у″ переводит нас в систему х′″, у′″, z′″; из (4.33) следует
Сочетая эти два последних преобразования, получаем
Подставляя сюда вместо С′+ и С′_ (4.32), придем к полному преобразованию
А если вспомнить, что
то эти формулы можно записать проще:
Это и есть наше искомое преобразование для поворота вокруг оси х на любой угол α. Оно лишь чуть посложнее остальных. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

 Вы, пожалуй, подумаете: «Это становится смешным. Чему же нас теперь будут учить — поворотам на 47° вокруг оси у, потом на 33° вокруг x? Долго ли это будет продолжаться?» Нет, оказывается, я почти все рассказал. Зная только два преобразования — на 90° вокруг оси у и на произвольный угол вокруг оси z (как вы помните, именно с этого мы начали),— мы уже способны производить любые повороты.
Вы, пожалуй, подумаете: «Это становится смешным. Чему же нас теперь будут учить — поворотам на 47° вокруг оси у, потом на 33° вокруг x? Долго ли это будет продолжаться?» Нет, оказывается, я почти все рассказал. Зная только два преобразования — на 90° вокруг оси у и на произвольный угол вокруг оси z (как вы помните, именно с этого мы начали),— мы уже способны производить любые повороты.