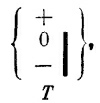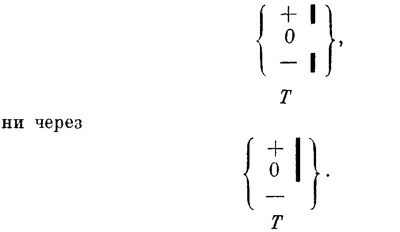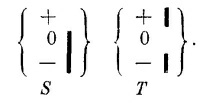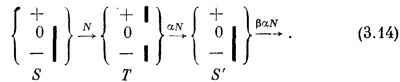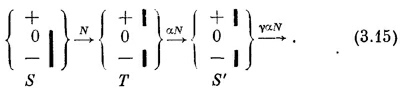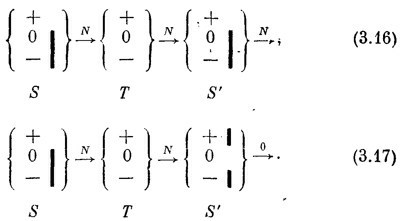| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Базисные состояния
Эти результаты иллюстрируют один из основных принципов квантовой механики: любая атомная система может быть разделена процессом фильтрования на определенную совокупность того, что мы назовем базисными состояниями, и будущее поведение атомов в любом данном отдельном базисном состоянии зависит только от природы базисного состояния — оно не зависит от предыдущей истории. Базисные состояния зависят, конечно, от примененного фильтра; например, три состояния (+Т), (0 Т) и (—Т)—это одна совокупность базисных состояний, а три состояния (+S), (0 S) и (—S) — другая. Возможностей сколько угодно, и ни одна не хуже другой.
но ни один из них не пройдет ни через
Наше утверждение относительно базисных состояний означает, что есть возможность отфильтровать пучок до некоторого чистого состояния, так что дальнейшее фильтрование идентичным прибором уже станет невозможным.
Атомы, выходящие из Т, оказываются в базисном состоянии (0Т) и не помнят, что когда-то они побывали в состоянии (+ S). Некоторые говорят, что при фильтровании прибором Т мы «потеряли информацию» о былом состоянии (+ S), потому что «возмутили» атомы, когда разделяли их прибором Т на три пучка. Но это неверно. Прошлая информация теряется не при разделении на три пучка, а тогда, когда ставятся перегородки, в чем можно убедиться в следующем ряде опытов.
Если наш третий прибор S′ выделяет другое состояние, скажем (0 S), то через него пройдет другая часть атомов, скажем γ. Мы будем иметь
Теперь предположим, что мы повторили оба эти опыта, убрав из Т все перегородки. Тогда мы получим следующий замечательный результат:
В первом случае через S′ прошли все атомы, во втором — ни одного! Это один из самых великих законов квантовой механики. То, что природа действует таким образом, вовсе не самоочевидно; результаты, которые мы привели, отвечают в нашем идеализированном случае квантовомеханическому поведению, наблюдавшемуся в бесчисленных экспериментах. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.