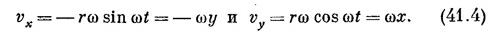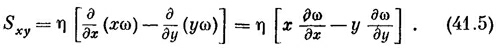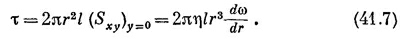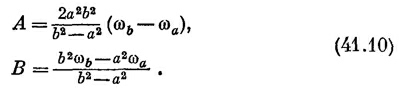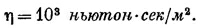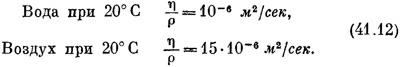| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Вязкость
В предыдущей главе мы говорили о поведении воды, пренебрегая при этом эффектами вязкости. Теперь же мне хотелось бы обсудить, как вязкость влияет на течение жидкости. Рассмотрим реальное поведение жидкости. Я опишу качественно, как ведет себя жидкость в самых разных условиях, так чтобы вы получше прочувствовали эту науку. И хотя вы увидите сложные уравнения и услышите о трудных вещах, наша цель совсем не в том, чтобы изучить все тонкости. Цель этой главы скорее «общеобразовательная», просто я хочу дать вам некоторое понятие о том, как устроен мир. Однако здесь все же есть один пункт, который стоит того, чтобы его выучить: полезно знать простое определение вязкости. С него мы и начнем. Все же остальное предназначено для вашего удовольствия.
В нашем приближении «сухой» воды мы отбрасывали последнее слагаемое, так что всеми эффектами вязкости мы пренебрегали. Кроме того, мы иногда делали еще дополнительное приближение, считая жидкость несжимаемой, и при этом получали дополнительное уравнение:
Это приближение часто оказывается вполне приличным, особенно когда скорость потока много меньше скорости звука. Но в реальных жидкостях мы почти никогда не можем пренебречь внутренним трением, называемым нами вязкостью; большинство интересных вещей в поведении жидкости так или иначе связано именно с этим свойством. Так, мы узнали, что циркуляция «сухой» воды никогда не изменяется: если ее не было вначале, то она никогда и не появится. Но в то же время мы повседневно сталкиваемся с циркуляцией в жидкости. Так что нашу теорию надо подправить.
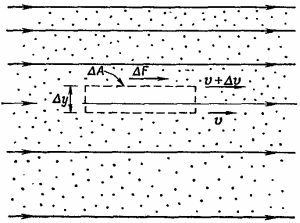
Далее, ∂vx/∂y представляет скорость изменения деформаций сдвига, определенных нами в гл. 38, так что силы в жидкости пропорциональны скорости изменения деформаций сдвига.
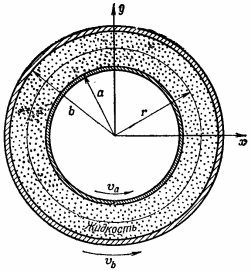
где ω = v/r. При этом х- и y-компоненты скорости равны
Из формулы (41.3) получаем
Для точек с у = 0 имеем дω/ду = 0, а x (дω/дх) будет равно r (dω/dr). Так что в этих точках
(Разумно думать, что величина S должна зависеть от ∂ω/∂r, когда ω не изменяется с r, жидкость находится в состоянии равномерного вращения и напряжения в ней не возникают.)
Поскольку движение воды стационарно и угловое ускорение отсутствует, то полный момент, действующий на цилиндрическую поверхность воды между радиусами r и r + dr, должен быть нулем; иначе говоря, момент сил на расстоянии r должен уравновешиваться равным ему и противоположно направленным моментом сил на расстоянии r + dr, так что τ не должно зависеть от r. Другими словами, r3 (dω/dr) равно некоторой постоянной, скажем А, и
Интегрируя, находим как ω изменяется с r:
Постоянные А и В должны определяться из условия, что ω = ωa в точке r = а, а ω = ωb в точке r = b. Тогда находим
Таким образом, ω как функция r нам известна, а стало быть, известно и v = ωr.
Он пропорционален относительной угловой скорости двух цилиндров. Имеется стандартный прибор для измерения коэффициентов вязкости, который устроен следующим образом: один из цилиндров (скажем, внешний) посажен на ось, но удерживается в неподвижном состоянии пружинным динамометром, который измеряет действующий на него момент сил, а внутренний цилиндр вращается с постоянной угловой скоростью. Коэффициент вязкости определяется при этом из формулы (41.11).
Часто удобнее бывает пользоваться удельной вязкостью, которая равна η, деленной на плотность ρ. При этом величины удельных вязкостей воды и воздуха сравнимы:
Обычно вязкость очень сильно зависит от температуры. Например, для воды непосредственно над точкой замерзания отношение η/ρ в 1,8 больше, чем при 20° С. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

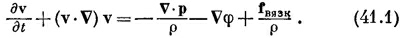
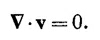
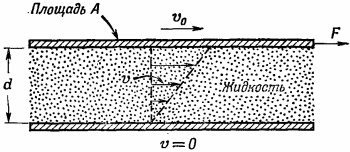 Сначала мы характеризовали жидкость так, что если приложить к ней напряжение сдвига, то, сколь бы мало оно ни было, жидкость «поддается» и течет. В статическом случае никаких напряжений сдвига нет. Однако, когда равновесия еще нет, в момент, когда вы давите на жидкость, силы сдвига вполне могут быть. Вязкость как раз и описывает эти силы, возникающие в движущейся жидкости. Чтобы измерить силы сдвига в процессе движения жидкости, рассмотрим такой эксперимент. Предположим, что имеются две плоские твердые пластины, между которыми находится вода (фиг. 41.1), причем одна из пластин неподвижна, тогда как другая движется параллельно ей с малой скоростью v0. Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отношению v0/d, где d — расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально v0/d:
Сначала мы характеризовали жидкость так, что если приложить к ней напряжение сдвига, то, сколь бы мало оно ни было, жидкость «поддается» и течет. В статическом случае никаких напряжений сдвига нет. Однако, когда равновесия еще нет, в момент, когда вы давите на жидкость, силы сдвига вполне могут быть. Вязкость как раз и описывает эти силы, возникающие в движущейся жидкости. Чтобы измерить силы сдвига в процессе движения жидкости, рассмотрим такой эксперимент. Предположим, что имеются две плоские твердые пластины, между которыми находится вода (фиг. 41.1), причем одна из пластин неподвижна, тогда как другая движется параллельно ей с малой скоростью v0. Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отношению v0/d, где d — расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально v0/d: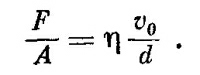
 Коэффициент пропорциональности η называется коэффициентом вязкости.
Коэффициент пропорциональности η называется коэффициентом вязкости.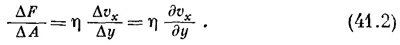
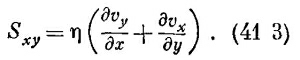
 При равномерном вращении жидкости производная ∂vx/∂y равна ∂vy/∂x с обратным знаком, a Sxy будет равна нулю, как это и требуется, ибо в равномерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проделывали в гл. 39 при определении еxy.) Разумеется, для Syz и Szx тоже есть соответствующие выражения.
При равномерном вращении жидкости производная ∂vx/∂y равна ∂vy/∂x с обратным знаком, a Sxy будет равна нулю, как это и требуется, ибо в равномерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проделывали в гл. 39 при определении еxy.) Разумеется, для Syz и Szx тоже есть соответствующие выражения.